Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 20
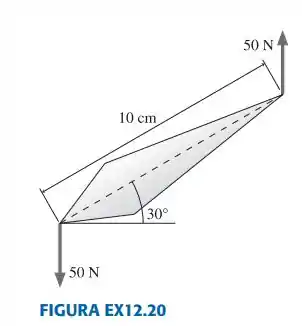
12.20. Na figura EX12.20, qual é o torque resultante em torno do centro de massa?
Passo 1
Vamos começar desenhando a figura
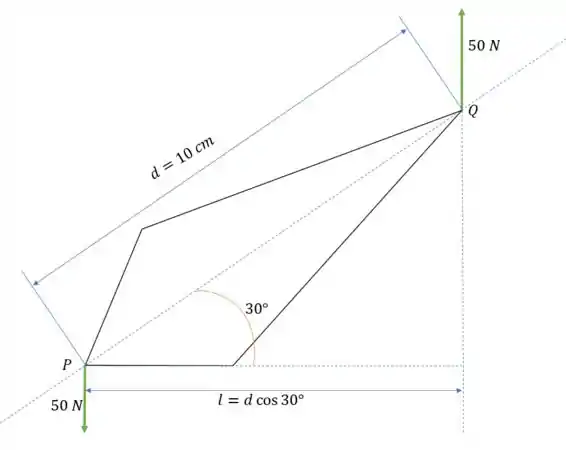
Nessa figura a gente nomeia os pontos “P” e “Q” na figura. Além disso, a gente determina o comprimento horizontal . Repare que é o comprimento na horizontal que é a projeção perpendicular de , por isso podemos assumir que .
Note que nesse exercício estamos tratando de um binário. As forças nos pontos “P” e “Q” são iguais em módulo, opostas e aplicadas nos dois extremos do objeto, isso que dizer que o objeto gira mas não translada.
Passo 2
Num caso binário, o torque resultante é o produto entre o módulo da força e a distancia entre as linhas de ação das duas forças.
Esse comprimento entre as duas linhas de ação é aquele comprimento que a gente chamou de . Com tudo isso, a gente já pode montar a equação:
Agora a gente substitui o valor de que tínhamos encontrado
Agora é só substituir os valores, mas sempre prestando atenção nas unidades de medida, vamos fazer
E esse é o torque.