Uma pequena bola com uma massa de está montada em uma das extremidades de uma barra de de comprimento e massa desprezível. O sistema gira e um círculo horizontal em torno da outra extremidade da barra a .
Calcule o momento de inércia do sistema em relação ao eixo de rotação.
Existe uma força de arrasto de agindo sobre a bola, no sentido oposto ao movimento. Que torque deve ser aplicado ao sistema para mantê-lo em rotação com velocidade constante?
Passo 1
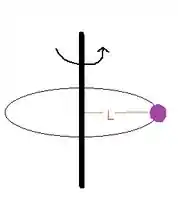
Para calcular o momento de inércia devemos primeiro ver que componentes tem massa não desprezível e estão em rotação. Bom, aqui só a bola tem massa considerável e ela está girando na extremidade da barra de comprimento ali do desenho. Então o momento de inércia vai ser dado só pela bola que está a uma distância do eixo de rotação:
Feito? Vamos pro próximo item?
Passo 2
Aqui o problema diz que tem uma força de arrasto, que funciona como um atrito, contrário ao movimento, e pergunta qual torque deve ser aplicado para manter a rotação constante.
Bom, sabemos que para manter uma velocidade constante, devemos ter uma aceleração nula. E isso não é diferente para rotações.
O torque aplicado deve ser igual e de sinal contrário ao torque oferecido pela força de arrasto, para anular seu efeito. Sendo assim, da seguna lei de Newton teremos:
Certo? Bora praticar mais?