Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 24

12.24. Um ginasta segura uma bola de 3,0 kg na mão. Seu braço tem 70 cm de comprimento e uma massa de 4,0 kg. Qual é o módulo do torque em torno do ombro se ele mantém o braço

a. Reto e paralelo ao solo?

b. Reto, porém formando 45° abaixo da horizontal?

Passo 1

Na situação “a” o ginasta está segurando a bola assim

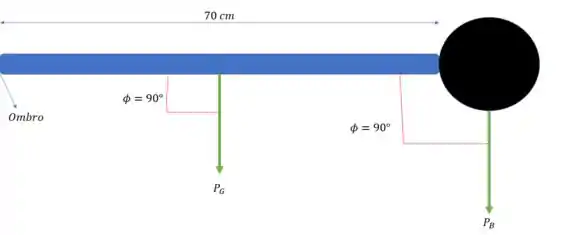
Vamos lá, o torque no ombro vai ser a soma dos torques gerados pelas forças peso da bola e do braço do ginasta.

τ = τ B + τ G

A gente que o módulo da força, então não tem problema colocar todos os valores positivos.

Começando com o torque gerado pelo peso da bola

τ B = P B d B sin ⁡ ϕ

A gente pode reescrever a força peso

τ B = m B g d B sin ⁡ ϕ

Agora vamos ver como fica o torque gerado pelo peso do braço do ginasta

τ G = P G d G sin ⁡ ϕ

τ G = m G g d G sin ⁡ ϕ

Agora a gente pode calcular o torque no ombro

τ = τ B + τ G

τ = m B g d B sin ⁡ ϕ + m G g d G sin ⁡ ϕ

Colocando g sin ⁡ ϕ em evidencia

τ = g sin ⁡ ϕ m B d B + m G d G

Agora é só substituir os valores

τ = 9,81 sin ⁡ 90 ° 3 0,7 + 4 0,35

τ = 34   N ⋅ m

Passo 2

Vamos para o item “b”. Agora o braço está nessa posição:

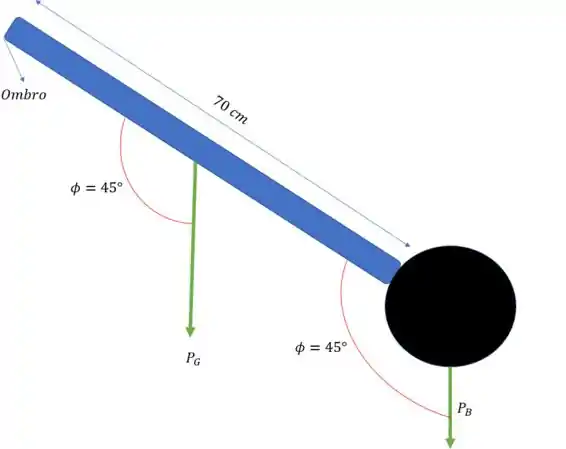
As condições iniciais são exatamente as mesmas que no item “a”, a única coisa que muda realmente é o ângulo. Então podemos usar a mesma equação que já usamos antes, mas agora o ângulo é diferente.

τ = g sin ⁡ ϕ m B d B + m G d G

Agora é só substituir os valores

τ = 9,81 sin ⁡ 45 ° 3 0,7 + 4 0,35

τ = 2 4   N ⋅ m

Resposta

  1. 34   N ⋅ m
  2. 24   N ⋅ m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Oito alunos de física, cujos pesos estão indicados em newtons na Figura, se equilibram em uma gangorra. Qual é o número do estudante que produz o maior torque em relação a um eixo de rotação que passa
Oito alunos de física, cujos pesos estão indicados em newtons na Figura, se equilibram em uma gangorra. Qual é o número do estudante que produz o maior torque em relação a um eixo de rotação que passa
O corpo da figura abaixo, pode girar em torno de um eixo que passa por O e é perpendicular ao papel e está submetido a três forças: FA=10 N no ponto A, a 8,0 m de O; FB=16 N em B, a 4,0 m de O; e FC=1
O corpo da figura abaixo, pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1=1,30 m, r2=2,15 m, F1=4,20 N, F2=4,90 N, θ 1
O comprimento do braço do pedal de uma bicicleta é 0,152 m e uma força de 111 N é aplicada ao pedal pelo ciclista. Qual é o módulo do torque em relação ao eixo do braço do pedal quando o braço faz um