Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 12.Exercícios e Problemas - Ex. 3
12.3P A caixa na Figura 12.9 tem massa de e seu coeficiente de atrito estático com a rampa é . A) Se , qual é o valor de para que ela fique em repouso? B) Suponha que seja aumentado para e a intensidade da força seja mantida no valor calculado anteriormente. Sendo o coeficiente de atrito cinético entre as superfícies, qual é a aceleração da caixa?
Passo 1
Belezoca galerinha, na letra (A) o enunciado nos diz que a rampa está inclinada , tal que as componentes da força normal , da força de atrito e da força peso estão representadas na figura, juntamente com a força que atua na horizontal:
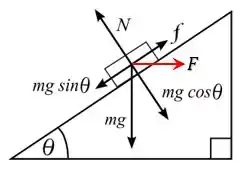
E se a gente fizer um diagrama de forças pro bloco nesse ponto, teremos:
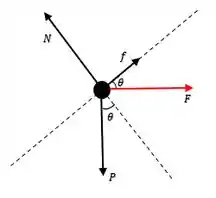
Belezoca, então para a caixa ficar em repouso, precisamos que as forças que atuam no eixo da rampa se anulem, ou seja, a força de atrito seja igual a componente da força gravitacional, sendo assim a aceleração nesse eixo será nula e o bloco não deslizará:
Passo 2
Iradoso, e como vimos neste capítulo, a força de atrito é dada pela expressão:
E essa força normal , é a resultante perpendicular à superfície. Devido a isso, vemos que tanto a força gravitacional quanto a força possuem componentes neste eixo, tal que:
De forma que a força de atrito pode ser expressa como:
Então o somatório das nossas forças no eixo da rampa é:
Passo 3
Mas calma lá meu patrão, a gente pode dar mais uma reorganizada nos termos, saca só:
Logo:
E como é a força da gravidade , temos que
Então se a gente substituir os valores que o enunciado deu pra gente, obtemos que:
Portanto a força para manter o bloco em repouso é:
Passo 4
Show de bolinhas, agora na letra (B), mudamos algumas coisinhas, primeiro que o ângulo inclinação agora é de , além disso o coeficiente de atrito cinético é dado por , mas em compensação a força se manteve fixa rsrs
E sabendo disso, queremos a aceleração resultante desse sistema.
Saca só jovem mancebo, vimos no item anterior que o somatório das forças no eixo da rampa era:
No item anterior, precisávamos que o corpo estivesse em repouso, por isso igualamos a expressão a , MAAAAASSS, agora vimos que o corpo vai possuir uma força resultante, de forma que também vai possui uma aceleração resultante , tal que:
Passo 5
Vimos também que a força de atrito poderia ser expressa em termos da força da gravidade e da força , de acordo com a expressão:
Então substituindo novamente a força de atrito na nossa expressão das forças, obtemos que:
E reorganizando, obtemos:
Logo a aceleração será:
E como , temos:
E então se a gente substituir os valores que a gente conhece, descobrimos que a aceleração vale:
