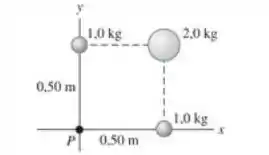
12.49. Três esferas uniformes estão fixadas nas posições indicadas na Figura 12.36. a) Determine o módulo, a direção e o sentido da força sobre uma partícula de 0,0150 kg situada no ponto P. b) Se essas esferas estivessem nas profundezas do espaço sideral e uma partícula de 0,0150 kg fosse libertada do repouso a 300 m da origem ao longo de uma reta a 45° abaixo do eixo , qual seria a velocidade da partícula quando ela atingisse a origem?
Passo 1
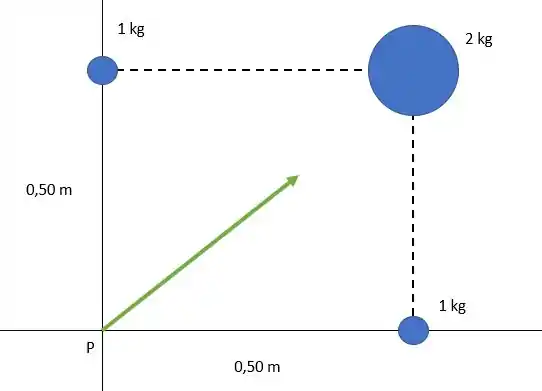
Vamos lá, o item (a) pede para gente calcular a força resultante sobre uma partícula no ponto P. Vão existir três forças agindo sobre essa partícula, resultado das três esferas que vão estar interagindo com ela. Então a situação fica assim
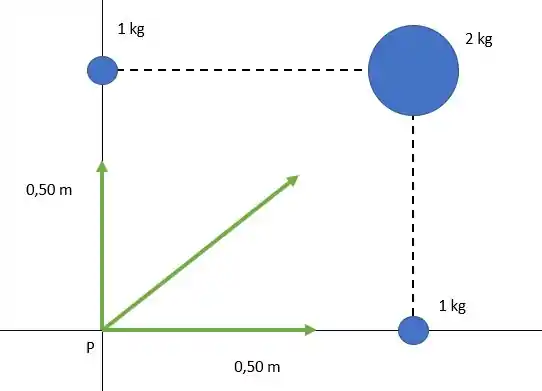
A força resultante será
Bom, pela simetria do problema, a gente pode ver que a força resultante terá a mesma direção e sentido que a força de interação entre a partícula e a massa de 2 kg.
Agora só nos resta calcular os módulos.
Passo 2
Podemos calcular o módulo da força gravitacional assim
Vamos começar calculando essa força
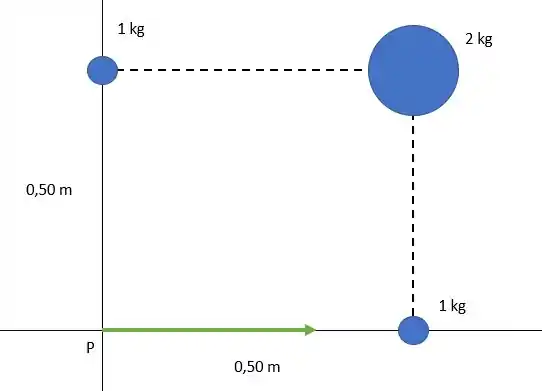
Isso vai dar
Agora
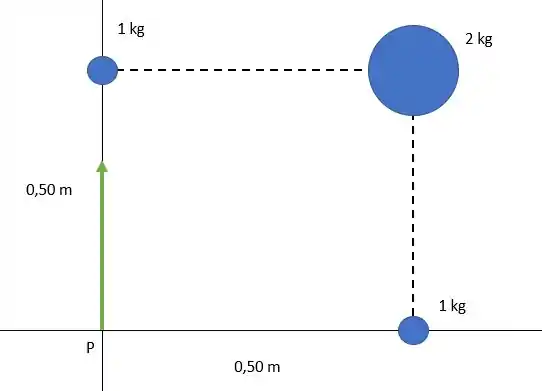
Repare pela simetria que o módulo é igual ao de
E como lá no primeiro passo a gente já concluiu que a força resultante tem direção e sentido igual a força entre a partícula P e a massa de 2 kg, ou seja 45° (a partir do eixo x ou y), a gente já pode calcular as componentes que vão somar na resultante.
Matematicamente, quero dizer
Então só falta calcular o módulo de
A gente pode achar a distância através de Pitágoras, já que podemos extrair um triângulo da imagem onde a gente sabe os dois catetos.
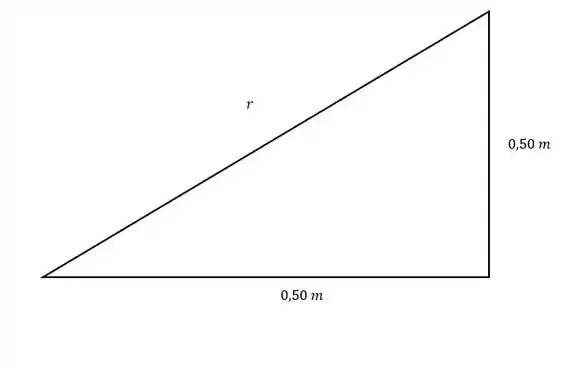
Então
Fazendo essa conta temos
Olha só
Mas o importante mesmo é que finalmente podemos calcular a força resultante
Então
Passo 3
Bem, agora vamos responder o item (b). Bom o enunciado descreve uma situação assim
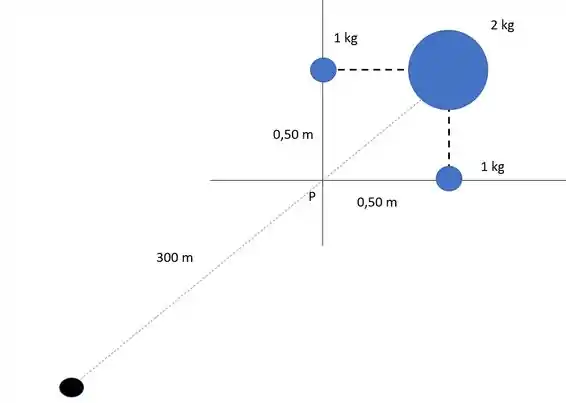
E a gente tem que descobrir a que velocidade a partícula passa pelo ponto P.
A gente pode usar o teorema do trabalho e energia cinética para resolver isso
Então
Bom a velocidade inicial é . A gente tem três forças agindo sobre a partícula. Então
Agora a gente só precisa isolar a velocidade
Só passar a raiz
Agora é só substituir os valores
Fazendo essa continha
Resposta
- Módulo:
Direção: Em direção a esfera de
Sentido: Positivo para eixo x e y