Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Problemas - Ex. 52
Em um dado instante, a Terra, a Lua e uma espaçonave de massa igual a ocupam os vértices de um triangulo equilátero de lado igual a . a) Determine o módulo, a direção o sentido da força gravitacional resultante exercida pela Terra e pela Lua sobre a espaçonave. Descreva a direção em termos do ângulo a partir da linha que liga a Terra com a espaçonave. Faça um diagrama mostrando a Terra, a Lua, a espaçonave e o vetor força. b) Qual seria o trabalho mínimo que você deveria realizar para afastar a espaçonave até uma distancia infinita da Terra e da Lua? Despreze os efeitos gravitacionais produzidos pelo Sol e pelos outros planetas.
Passo 1
A força da gravidade para cada par de objetos é dada pela equação da lei da gravitação
O trabalho realizado .
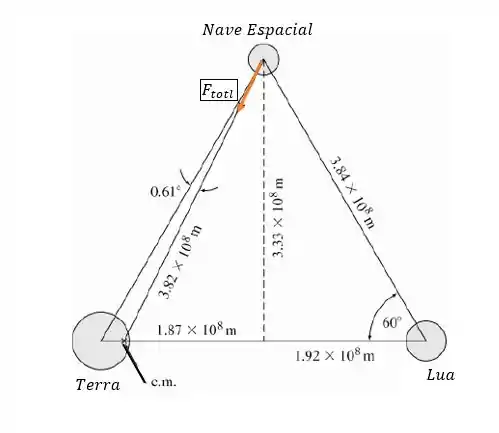
A maneira mais simples de abordar esse problema é encontrar a força entre a espaçonave e o centro da massa do sistema terra-lua, que é do centro da terra. A distância do
nave espacial para o centro de massa do sistema terra-lua é
Passo 2
- Usando a Lei da Gravitação, a força na sonda é de , um ângulo de da linha da sonda terrestre.
Passo 3
E
para a nave espacial e a terra, e a nave espacial e a lua.