Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 4.Problemas Adicionais - Ex. 126
126- O módulo da velocidade de um projétil quando ele atinge a altura máxima é 10 m/s.
(a) Qual é o módulo da velocidade do projétil 1,0 s antes de atingir a altura máxima?
(b) Qual é o módulo da velocidade do projétil 1,0 s depois de atingir a altura máxima? Se tomamos x = 0 e y = 0 como o ponto de altura máxima e consideramos como sentido positivo do eixo x o sentido da velocidade do projétil nesse ponto,
determine (c) a coordenada x e (d) a coordenada y do projétil 1,0 s antes de atingir a altura máxima e (e) a coordenada x e (f) a coordenada y do projétil 1,0 s depois de atingir a altura máxima.
Passo 1
Quando atinge a altura máxima o projétil tem somente a coordenada horizontal da velocidade, e que é constante ao longo de toda a trajetória, logo:
Sabendo que a velocidade em qualquer ponto dessa trajetória pode ser encontrada por:
E assumindo que o ponto inicial de análise é justamente o ponto de máxima altura da bala, então 1 segundo antes temos a seguinte velocidade.
a)
Pois um segundo antes do momento inicial é .
O que nos dará uma componente de velocidade total igual a:
b) Um segundo depois temos a seguinte expressão para a velocidade vertical.
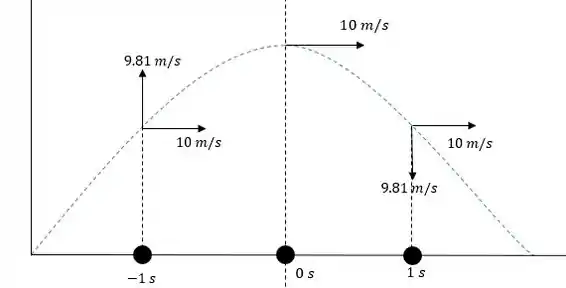
Passo 2
Tomando como origem o ponto de altura máximo temos que a coordenada 1 segundo após será de:
e)
E a coordenada segundo antes será de:
c)
Passo 3
As coordenadas verticais do projétil antes e depois do ponto de máximo serão calculados por:
Como e logo as coordenadas verticais do projeteis terão o mesmo valor.