Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 50

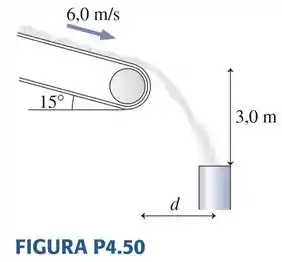
Areia se move a 6,0   m / s , sem escorregar, sobre um esteira rolante inclinada para baixo em 15°. A areia entra, então, em um tubo cuja extra cidade mais alta está 3,0 m abaixo do final da esteira rolante, como mostra a FIGURA P4.50. Qual é a distância horizontal d entre a esteira e o cano?

Passo 1

Esquematizando o movimento

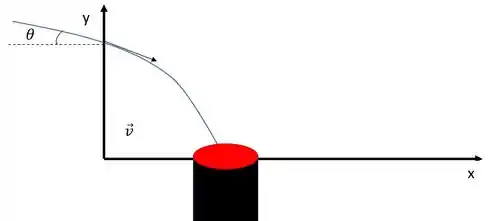
E sabemos que

x 0 = 0

y 0 = 3   m

t 0 = 0

v 0 = 6   m / s

θ = 15 °

a y = - g

E temos que encontra o x

Passo 2

O movimento em y é uniforme variado, então vamos substituir na equação os dados que sabemos até agora, e ah, o y = 0 porque estamos considerando que ele chegou na altura do chão

y = y 0 + v 0 y t - t 0 - g t - t 0 2 2 → 0 = 3 + v 0 y t - 4,9 t 2

Mas vamos substituir o v 0 y ? Maas, como o ângulo está a baixo do movimento, temos que inverter o sinal, da seguinte forma

v 0 y = v 0   s e n   θ = - 6   s e n   15 ° = - 6 × 0,258 = - 1,55   m / s

Voltando na formula

0 = 3 + v 0 y t - 4,9 t 2 → 3 - 1,55 t - 4,9 t 2 = 0

Resolvendo a equação encontramos duas soluções para t , que é 0,6399   s e - 0,956   s , entretanto, como não existe tempos negativos, usaremos a primeira opção. A velocidade em relação a x é

v 0 x = v 0 cos ⁡ θ = 6 cos ⁡ 15 ° = 6 × 0,965 = 5,79   m / s

Usando a formulazinha em relação a x, que é um movimento uniforme

x = x 0 + v 0 x t - t 0 → x = 0 + 5,79 × 0,6399 → x = 3,70   m

Resposta

3,7 0   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um parque de diversões você pode ganhar uma girafa inflável, se conseguir encaixar uma moeda de 25 centavos em um prato pequeno. O prato está sobre uma prateleira acima do ponto em que a moeda deix
Um homem está parado no alto de um edifício de 15,0m de altura e atira uma pedra com velocidade de módulo de 30,0m / s formando um ângulo inicial de 33,0 ° acima da horizontal.Despreze a resistência d
Mark McGwire bate uma bola de beisebol de forma que ela abandona o bastão com velocidade de 30,0m / s formando um ângulo de 36,9 ° acima da horizontal. Despreze a resistência do ar. a) Ache os dois in
Um projétil é disparado a 35 ° acima da horizontal. Quaisquer efeitos devidos à resistência do ar são desprezíveis. A velocidade inicial do projétil no problema 20 tem um componente vertical que é (a)
A figura representa a trajetória parabólica de um projétil indo de A até E . A resistência do ar é desprezível. Qual é a direção da aceleração no ponto (b)? (a) Para cima e para a direita, (b) para ba