Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 42
Um projétil é disparado com velocidade inicial de 30 m/s em um ângulo de 60° acima da horizontal. O projétil atinge o solo 7,5 s mais tarde.
a. A que altura acima ou abaixo do ponto de lançamento o projetil atinge o solo?
b. A que altura máxima acima do ponto de lançamento o projétil se eleva?
c. Qual é o módulo e a orientação da velocidade do projetil no instante em que ele atinge o solo?
Passo 1
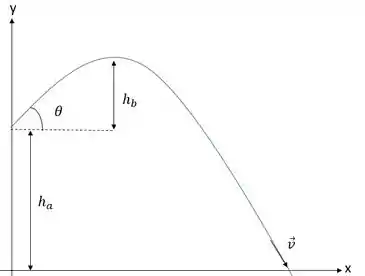
Vamos pegar os dados e fazer um esqueminha para começar o problema
Lembrando que o movimento é uma parábola! Em (a) ele pede a diferença de altura do ponto inicial, em (b) pede a altura máxima, então vamos descobrir e somar com ! E por último o vetor quando está prestes a chegar no chão! Vamos lá!
Passo 2
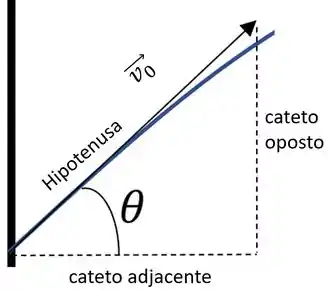
- A velocidade pode ser interpretada em relação ao eixo y e em relação ao eixo x! Assim, se ampliarmos o vetor velocidade, ele faz um triângulo. Então em relação ao eixo x
- Para descobrir a altura máxima usaremos a seguinte fórmula:
- Para saber o módulo das velocidades e para saber o ângulo, temos que descobrir os valores dos componentes x e y.
Com o mesmo raciocínio podemos supor que
Primeiro queremos descobri qual é o que é , então, consideremos o movimento vertical
Mas porque é negativo? Estamos considerando que o eixo y para cima é positivo. Logo a interpretação é que o projétil está a 80,8 m abaixo de onde foi lançado!
Passo 3
Em relação ao ponto inicial a altura é de 34,4 m. Mas se considerarmos em relação ao solo temos
A altura máxima é de 115,2 m!
Passo 4
Em x, o movimento é retilíneo e uniforme, então, o vetor velocidade de x é constante em todo o trajeto, ou seja, o vetor velocidade inicial é igual ao final! Colocando na formulazinha:
E em y, o movimento já muda um pouquinho, nesse caso, o movimento é uma queda livre, então usamos:
Daí pra descobri o módulo, colocamos dentro da raiz
Portanto o módulo da velocidade é de 50 m/s!
Passo 3
Continuando o item (c) e descobrir o ângulo, vamos voltar nesse esquema
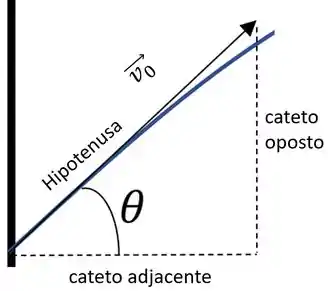
E para descobrir o ângulo, vamos usar
Mas como estamos trabalhando com os vetores velocidades, o cateto oposto representa nosso vetor y, e o cateto adjacente o vetor velocidade x, temos:
Assim, sua posição é de 73° em relação ao chão.
Resposta
- e