Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 52

Um dublê dirige um carro a 20 m/s em direção à beira de um penhasco de 30 m de altura. A estrada que leva ao penhasco é inclinada para cima em um ângulo de 20°.

a. A que distância da base do penhasco o carro aterrissará?

b. Qual é o módulo da velocidade de impacto do carro?

Passo 1

Os dados fornecidos

v 0 = 20   m / s

x 0 = 30   m

θ = 20 °

E esquematizando o movimento, desde quando o duble anda na estrada até a trajetória parabólica do movimento

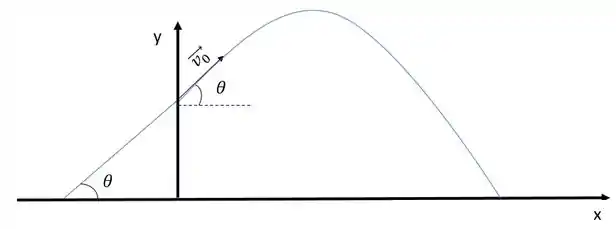
E temos que lembrar também que em relação a x é Movimento Uniforme, e em y é Movimento Uniformemente Variado, porque existe a aceleração da gravidade. O exercício pede para encontra o x e o módulo da velocidade do impacto

Passo 2

  1. Começando, vamos decompor a velocidade inicial em relação a x e a y

    2. v 0 x = v 0 cos ⁡ 20 ° = 18,79   m / s

    v 0 y = v 0 sen ⁡ 20 ° = 6,84   m / s

    Assim, substituímos na equação do movimento em relação a y, porque ele que define o tempo do movimento

    y = y 0 + v 0 y t - t 0 + a y t - t 0 2 2 → 0 = 30 + 6,84 t - 4,9 t 2

    Encontra-se t 1 = 3,269   s e o outro t é negativo o que é impossível fisicamente, portanto, utilizamos   t 1 .

    Continuando, como encontramos o tempo total do movimento, podemos encaixar em relação a x para determinar a distancia

    x = x 0 + v 0 x t - t 0 → x = 18,79   .   3,269 = 61,4   m

    O alcance foi de 61,4 m.

    Passo 3

  2. Para saber o módulo da velocidade temos que encontrar v x e v y . O movimento em relação a x é constante, então podemos dizer que

v 0 x = v x = 18,79   m / s

E em y podemos usar usa equação do movimento, porque existe variação da velocidade ao longo do trajeto

v y = v 0 y - g t → v = 6,84 - 9,8 × 3,269 = 25,2   m

Colocando a velocidade

v = 18,99 2 + 25,2 2 = 31,4   m / s

Descobrimos o módulo da velocidade!!

Resposta

  1. 61,4   m
  2. 31,4 m/s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola é lançada do nível do chão e volta ao chão, no mesmo nível, 2,44 s após, a uma distância de 40,0 m do ponto de lançamento. Encontre a magnitude do vetor velocidade inicial e o ângulo que ele
Uma bala de canhão é disparada com uma rapidez inicial v 0 a um ângulo de 30° acima da horizontal, de uma altura de 40 m acima do chão. O projétil chega ao chão com uma rapidez de 1,2 v 0 . Encontre v
A 1 2 de sua altura máxima, a rapidez de um projétil é 3 4 de sua rapidez inicial. Qual foi o ângulo de lançamento? (Ignore a resistência do ar.)
Um projétil é lançado com a rapidez v 0 a um ângulo θ 0 acima da horizontal. Encontre uma expressão para a altura máxima que ele atinge, acima do ponto de lançamento, em função de v 0 ,θ e g . (Ignore
Considere uma bola lançada do chão com uma rapidez inicial v 0 a um ângulo θ 0 acima da horizontal. Chamando de v a rapidez a uma altura h acima do chão, mostre que, para um dado valor de h ,v é indep