Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 54

Uma linha de montagem possui um grampeador que se desloca para a esquerda com 1,0 m/s enquanto as partes a serem grampeadas deslocam-se para a direita a 3,0 m/s. O grampeador insere 10 grampos por segundo. A que distância um do outro os grampos serão inseridos?

Passo 1

Vamos assumir que o movimento é horizontal e está diretamente ligado ao eixo x. Interpretado o enunciado, a velocidade das partes vai para a direita com valor de 3,0 m/s e do grampeador a esquerda com velocidade de 1,0 m/s como podemos ver na figura a baixo

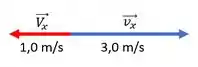
E nossos vetores são

v x → = v e l o c i d a d e   d a s   p a r t e s   a   s e r e m   g r a m p e a d a s = 3   m / s

V x → =   v e l o c i d a d e   d o m   g r a m p e a d o r   = - 1   m / s

Assim, utilizando a soma de Galileu para a velocidade que consiste em uma soma de vetores, podemos dizer que

v ' x → = v x → + V x →

Entretanto, os dois estão da mesma direção, mas em sentidos contrários! Quando é assim, podemos simplesmente fazer a subtração! Como o vetor azul está para a esquerda, vamos considerar ele positivo, e o vetor vermelho negativo, assim

v x → = 3 - - 1

v x → = 4 , 0   m / s

E podemos verificar graficamente o vetor resultante

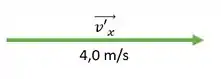
Passo 2

O tempo é descrito como 10 grampos por 1 segundo, então para inserir um grampo leva 0,1 , como pode ser visto pela regra de 3

1 0   g r a m p o - - - 1 s

1   g r a m p o - - - t

t = 1 10 s = 0,1   s

E, finalmente, para saber a distância dos grampos

V e l o c i d a d e   t o t a l = d i s t â n c i a   e n t r e   d o i s   g r a m p o s t e m p o   e n t r e   d o i s   g r a m p o s → 4 = d i s t â n c i a 0,1   →

d i s t a n c i a = 4 × 0,1 = 0,4   m

Resposta

0,4 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura representa a trajetória parabólica de um projétil indo de A até E . A resistência do ar é desprezível. (a) Em quais pontos a rapidez é máxima? (b) Em quais pontos a rapidez é mínima? (c) Em q
Dois canhões estão apontados um para o outro, como mostrado na figura. Quando são disparadas, as bolas dos canhões vão seguir as trajetórias mostradas – P é o ponto onde as trajetórias se cruzam. Se q
Estime a distância a que você pode jogar uma bola se você a jogar (a) horizontalmente ao nível do solo, (b) Com θ = 45 ° acima da horizontal, enquanto está de pé no nível do solo, (c) horizontalmente
Você faz um arremesso, lançando uma bola de beisebol a 87 mi/h até a base, que está distante 18,4 m. Quanto a bola terá caído, por efeito da gravidade, ao chegar à base? (Ignore a resistência do ar.)
Um malabarista, viajando em um trem, atira uma bola verticalmente para cima, em relação ao trem, com uma rapidez de 4,90 m/s. O trem tem uma velocidade de 20 m/s para o leste. Como visto pelo malabari