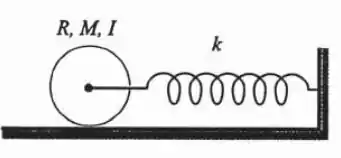
13.10P Quando forçado pela mola, a roda vista na Figura 13.16 rola sobre o piso, girando em torno de seu eixo. Calcule a frequência de oscilação do sistema.

Mas saca só a sagacidade, o enunciado nos diz que quando forçado pela mola a roda rola pelo chão girando em torno de seu eixo, e se ela rola, então sabemos que é sem deslizar. Isso quer dizer que quem causa o movimento na roda, é a força elástica produzida pela mola:

MAAAASSSS, como a roda está rolando pelo chão, quer dizer que existe uma força de atrito oposta ao movimento e a força elástica que causa o torque necessário para colocar a roda em rolamento:

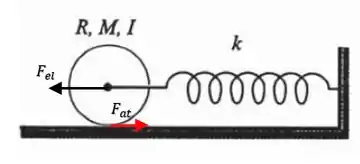
E como essa força de atrito exerce o torque em relação a um raio da roda, temos que:

Só que o torque também pode ser expresso através da fórmula:

Onde é a aceleração angular e é o momento de inércia da roda. Nesse caso, a aceleração angular pode ser relacionado com a aceleração linear pela relação . Dessa maneira, se a gente igualar os torques, teremos que:

Logo a força de atrito é:

E como só temos a força elástica e a força de atrito atuando no sistema, a força resultante será:

Logo, dada aceleração resultante , temos:

Iradoso, então se a gente substituir as informações que a gente encontrou, vamos ter que:

Mas calma lá chefia, porque agora vem o golpe final. Lembra que esse sistema está oscilando?! Então, isso quer dizer que ele obedece às equações do movimento harmônico simples, para posição e aceleração, tal que:

Então substituindo essas expressões, na nossa equação, temos que:

Logo, como se repete em todos os elementos, podemos cortar ele da equação, tal que:

Logo, isolando a velocidade angular , teremos:

Mas calma lá jovem mancebo, ainda não acabou. Porque incialmente queríamos encontrar a frequência de oscilação, e descobrimos que ela era dada em função da velocidade :

E agora que encontramos essa velocidade angular, temos que a frequência será: