Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 13.Exercícios e Problemas - Ex. 8
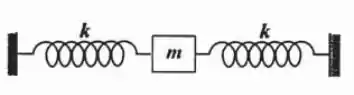
13.8P Calcule a frequência de oscilação do sistema apresentado na Figura 13.14.
Passo 1
Show de bolinhas galera bonita, o enunciado pede pra gente calcular a frequência de oscilação do sistema apresentado na figura:
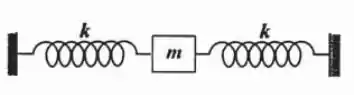
Mas beleza, a frequência do movimento é dada pela relação:
Onde é o período do movimento, que pode ser expresso através da relação com a velocidade angular :
Ou seja, depois de toda essa volta que a gente deu, descobrimos que na verdade a frequência pode ser expressa em termos de :
Então bora lá encontrar essa velocidade angular!!
Passo 2
Belejóia pessoal, a velocidade angular de um sistema massa-mola comum, onde possuímos apenas mola, de constante , e massa , a velocidade angular é dada pela expressão:
MAAAASSSS, a malandragem nesse caso aqui, é que temos duas molas de constante atuando sobre a mesma massa , isso faz com que a força elástica que cada mola exerce sobre a massa , se sobreponham.
Dessa maneira podemos tratar o sistema como possuindo apenas mola, só que de constante elástica , que equivale a soma das constantes de cada mola! Sendo assim, a velocidade angular do sistema será:
Passo 3
Iradoso, então agora que a gente descobriu a velocidade angular, podemos dizer que a frequência do movimento é dada por:
