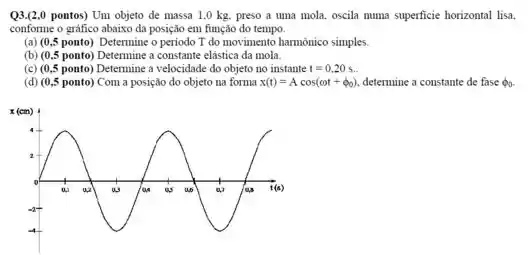
Exercícios de Oscilador Linear Massa-Mola - Lista de Exercícios Resolvida
Questão 1
Um oscilador é formado por um bloco preso a uma mola ). Em um certo instante a posição (medida a partir da posição de equilíbrio do sistema), e a aceleração do bloco são , e . Calcule
(a) a frequência de oscilação,
(b) a massa do bloco
Ver solução completaQuestão 2
Uma pedra de está oscilando na extremidade inferior de uma mola vertical. Se a maior velocidade da pedra é 15,0 cm/s e o período é de , determine:
(a) a constante elástica da mola
(b) a amplitude do movimento
(c) a frequência da oscilação.
Ver solução completaQuestão 3
Um oscilador é formado por um bloco com uma massa de ligado a uma mola. Quando é posto em oscilação com uma amplitude de o oscilador repete o movimento a cada . Determine:
(a) o período
(b) a frequência
(c) a frequência angular
(d) a constante elástica
(e) a velocidade máxima
(f) o módulo da força máxima que a mola exerce sobre o bloco.
Ver solução completaQuestão 4
As missões Apollo 15, 16 e 17 levaram um jipe para a superfície lunar. Esse jipe quando totalmente carregado possui uma massa , a mola da suspensão possui uma frequência natural de oscilação de medidos na superfície terrestre. Sabendo que a aceleração da gravidade na superfície lunar equivale a ao da aceleração na superfície terrestre, pode-se afirmar que a frequência natural de oscilação da suspensão do jipe na superfície lunar é
- Depende da massa do jipe,
Questão 5
Um sistema massa-mola consiste em um bloco de massa preso a uma dada mola. Sabe-se que o sistema oscila com amplitude de e que ele repete seu movimento a cada . Suponha que a posição seja dada por . Se a posição do bloco em é a maior possível, determine:
O período e a frequência angular do movimento;
A constante da mola;
A velocidade máxima;
A constante de fase ;
Ver solução completaQuestão 6
Um sistema massa+mola descreve um deslizando em uma superfície horizontal com atrito desprezível que obedece à seguinte equação:
Considere a força elástica da mola dada por e determine:
- O vetor posição inicial do bloco.
- O vetor aceleração do bloco no instante
Questão 7
Uma forma de medir a massa de um objeto em uma estação espacial é o seguinte: primeiro, o astronauta mede a frequência de oscilação de um sistema elástico de massa conhecida. Depois, a massa desconhecida é adicionada a esse sistema e uma nova medida de frequência de oscilação é tomada. Qual o valor de ?
Questão 8
Um bloco suspenso por uma mola ideal se desloca com pequenas oscilações para cima e para baixo com período igual a na Terra. Se você levar esse bloco para Marte onde a aceleração da gravidade é da aceleração da gravidade da Terra, considere as afirmações:
-O período permanecerá o mesmo pois só depende da massa do bloco e da constante elástica da mola.
-A mola, na sua nova posição de equilíbrio irá se esticar de um comprimento menor em Marte do que na Terra.
-O período irá diminuir pois é proporcional à raiz quadrada de
Quais das afirmações acima são verdadeiras?
- Somente
- Somente
- Somente
- Somente e
- Somente e
Questão 9
Coloca-se um bloco em uma balança, composta por um prato apoiado sobre uma mola, deslocando sua posição de equilíbrio de . Em seguida, um pequeno impulso faz a balança oscilar harmonicamente. Desconsiderando-se efeitos de amortecimento e o peso do prato da balança, e considerando a aceleração da gravidade , qual deve ser a frequência angular de oscilação do sistema balança-bloco?
Questão 10
Consideramos uma mola com 2 constantes elásticas: , quando é esticada e , quando comprimida:
Suponha que esta mola seja presa a um bloco de massa que pode oscilar sobre uma superfície horizontal sem atrito. O período de oscilação do sistema é:
Questão 11
Uma massa desconhecida é suspensa por uma mola de constante elástica desconhecida de modo que a força elástica equilibra o peso dessa massa. Sabendo-se apenas o valor da distensão sofrida pela mola, é correto afirmar que:
- Somente a constante elástica da mola pode ser determinada.
- Podem-se determinar a velocidade máxima e o período desse sistema massa-mola.
- O período desse sistema massa-mola poderá ser determinado.
- Podem-se determinar a constante elástica da mola e o príodo desse sistema massa-mola.
- Nada pode ser determinado.
Questão 12
O processo descrito a seguir tem sido realmente usado para “pesar” astronautas no espaço. Uma cadeira de 42,5 kg é presa a uma mola e deixada oscilar livremente. Quando vazia, a cadeira leva 1,30 s para completar uma oscilação. Mas, com uma astronauta sentada nela, sem apoiar os pés no chão, a cadeira leva 2,00 s para completar um ciclo. Qual é a massa da astronauta?
Ver solução completaQuestão 14
Um corpo de massa está preso a uma mola vertical de constante elástica de . Quando ele é puxado até abaixo do equilíbrio e largado do repouso, ele oscila com frequência de .
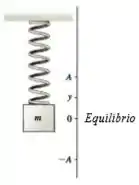
- Determine massa do corpo.
- Determine de quanto a mola está distendida, quando o corpo está em equilíbrio.
- Escreva a expressão para a posição como função do tempo para o movimento oscilatório, sendo o tempo inicial quando o corpo é largado.
Questão 15
Considere um sistema bloco-mola que está ligado verticalmente a um teto, o qual pode ser instala do em diferentes planetas. Seja e a posição de equilíbrio e frequência angular de oscilação do sistema bloco-mola, respectivamente, no caso do teto ser instalado na Terra. Por outro lado, e são as mesmas quantidades no caso do teto ser instalado em Marte. A aceleração da gravidade em Marte é aproximadamente vezes menor que na Terra. Pode-se dizer que:
Nenhuma das anteriores.
Ver solução completaQuestão 16
Uma barra delgada e homogênea de massa M possui um pivô em uma das extremidades e na outra, uma mola vertical de constante elástica k. Mostre que a barra, quando deslocada de um pequeno ângulo de sua posição de equilíbrio horizontal e liberada, realiza um movimento harmônico simples de frequência angular .
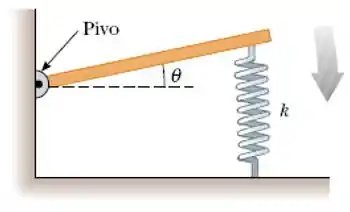
Questão 17
Um bloco de massa M preso a uma mola de constante elástica k descreve um movimento harmônico simples horizontal com amplitude . No instante em que o bloco passa pela posição de equilíbrio, um pedaço de massa de vidraceiro, de massa m, cai verticalmente de uma pequena altura sobre o bloco e gruda nele.
a) Calcule a nova amplitude e o novo período.
b) Repita o item (a) supondo que a massa caia sobre o bloco no instante em que ele está na extremidade de sua trajetória.
Ver solução completaQuestão 18
Um bloco de 0,20 kg está preso a uma mola ideal de constante elástica de 28,8 N/m executando um movimento harmônico simples horizontal. Em t = 0 o bloco passa pela sua posição de equilíbrio (x = 0) com velocidade de 1,2 m/s no sentido negativo do eixo x. Escreva a equação da posição em função do tempo.
Ver solução completaQuestão 19
Um único sistema massa-mola é colocado para oscilar de três maneiras diferentes. No caso (A), o sistema está alinhado verticalmente, com uma extremidade da mola presa ao teto, no caso (B), horizontalmente com a massa deslocando-se sobre uma superfície sem atrito e finalmente no caso (C), em um plano inclinado de um ângulo , onde a massa desloca-se sobre a superfície também sem atrito. Denominado-se as frequências angulares para cada maneira como respectivamente, é correta a opção:
- ;
- ;
- ;
Questão 20
Um corpo efetua um movimento harmônico simples linear (MHS), quando numa trajetória retilínea, oscila periodicamente em torno de sua posição de equilíbrio sob ação da força restauradora cuja intensidade é proporcional à distância do corpo ao ponto de equilíbrio. A figura ilustra um corpo de massa m preso a uma mola de constante elástica k que será abandonado da posição x= 2m para dar início ao MHS em torno da posição de equilíbrio x=0, com freqüência angular de 1 rad/s.
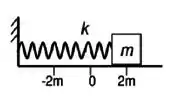
Despreza-se qualquer tipo de atrito ao movimento do corpo. Indique o gráfico que representa a função horária da velocidade do corpo de massa m em um período completo (T) de oscilação.
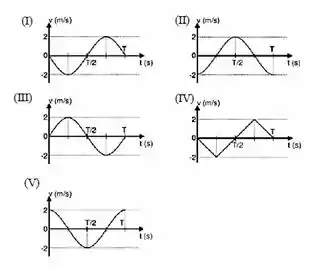
(a) Figura (I)
(b) Figura (II)
(c) Figura (III)
(d) Figura (IV)
(e) Figura (V)
Ver solução completaQuestão 21
Uma mola ideal sem massa de constante elástica está presa a um bloco de massa que pode deslizar sobre uma superfície horizontal sem atrito. No instante o bloco é liberado a partir do repouso da posição . Pode-se afirmar que período do movimento:
- Independente das condições iniciais do problema
- Função da energia mecânica do oscilador
- Inversamente proporcional a constante elástica
- Proporcional a amplitude de oscilação
- Proporcional a massa do bloco
Questão 23
Uma mola ideal, de comprimento relaxado e constante elástica k tem um de seus extremos presos ao teto de um laboratório. Para um pequeno bloco de massa é conectado à extremidade livre da mola e o sistema permanece em equilíbrio na posição num eixo cuja origem corresponde ao ponto em que a mola não tem deformação, como mostrado na figura (). A uma altura abaixo desta posição há um dispositivo sensível ao toque que acende uma lâmpada cada vez que é tocado pelo bloco como pode ser visto na figura (). Em você encosta o bloco no dispositivo e o libera a partir do repouso. Despreze quaisquer forças dissipativas no sistema, utilize o eixo da figura () e JUSTIFIQUE todas as respostas. Suponha a gravidade conhecida.
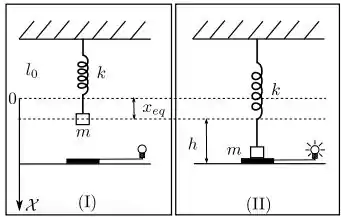
Responda aos QUATRO itens abaixo:
1. Calcule .
2. Obtenha a equação diferencial do movimento do bloco para .
3. Considere, APENAS NESTE ITEM, que . Para que valor da constante elástica da mola a lâmpada acende em intervalos de tempo de segundo?
4. Determine a função de movimento do bloco para
USANDO AS CONDIÇÕES INICIAIS.
Ver solução completaQuestão 24
O gráfico mostra a posição em função do tempo de uma partícula de massa , ligada a uma mola de massa desprezível, que move-se em movimento retilíneo, sobre uma mesa horizontal lisa, na direção do eixo x, orientado para a direita.
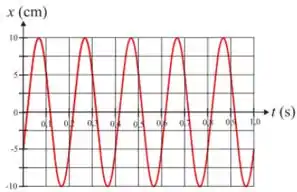
. Podemos afirmar que o instante exato que a partícula estará passando pelo ponto de equilíbrio e movendo-se para a direita, durante o primeiro período do movimento, é:
Ver solução completaQuestão 25
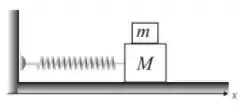
. Um bloco de massa está ligado a uma mola de constante elástica e apóia-se sobre um plano horizontal sem atrito. Um outro bloco, de massa , está no topo do bloco de massa . Se o coeficiente de atrito estático entre os dois corpos é , a distância máxima que os dois corpos podem ser puxados a partir da posição de equilíbrio sem que o bloco de cima escorregue, uma vez que os dois sejam librados é:
Questão 26
Uma mola ideal de constante elástica está fixada ao solo, mantendo-se na posição vertical. Ela tem na sua parte superior um prato, de massa desprezível. O comprimento da mola nesta situação inicial, sem deformação, vale . Uma pessoa segura um objeto de massa encostada no prato e o abandona. O objeto fica nele grudado, passando este sistema massa+mola a oscilar verticalmente.
a) Determine a posição vertical yeq em relação ao solo em torno da qual o sistema irá oscilar.
b) Tomando este ponto como nova origem, escreva a expressão para a deformação da mola numa posição qualquer.
c) Obtenha a equação diferencial para que governa este movimento de oscilação.
d) Considerando o instante em que o objeto é abandonado sobre o prato, e usando a nova origem introduzida no item b), escreva as condições iniciais deste movimento de oscilação.
e) Escreva a função horária que descreve este movimento na forma , deixando claro as expressões para a frequência angular, para a amplitude, e para a constante de fase.
Ver solução completaQuestão 27
Um bloco de massa m está conectado a uma mola de constante elástica em um plano inclinado que forma um ângulo em relação à horizontal. No instante , o bloco é solto da posição , com velocidade inicial nula. Considerando que a mola está relaxada (nem comprimida, nem esticada) quando , determine:
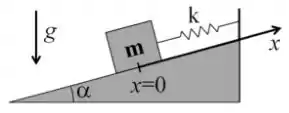
(a) A equação do movimento do bloco ao longo do eixo x mostrado na figura.
(b) A posição da massa em função do tempo. Qual é a amplitude do movimento e os valores máximo () e mínimo ( de ?
(c) A energia cinética em função do tempo.
Ver solução completaQuestão 28
Uma mola se distende de quando uma massa de é pendurada nela. Quando uma massa de é presa a ela, e realiza um movimento harmônico simples, qual o período deste movimento?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 29
Consideremos uma mola com 2 constantes elásticas: , quando é esticada e , quando comprimida, tal que:
Suponha que esta mola seja presa a um bloco de massa que pode oscilar sobre uma superfície horizontal sem atrito. O período de oscilação do sistema é:
- Nenhuma das alternativas acima.
Questão 30
Um móvel executa MHS e obedece à função horária , no SI. O tempo necessário para que este móvel vá da posição de equilíbrio para a posição de elongação máxima e o valor da aceleração no instante t são, respectivamente:
(a) 1 s e - cos(π/2t+π)
(b) 1 s e - π cos(2π/2t+2π)
(c) 2 s e - cos(π/2t+π)
(d) 1 s e - cos(3π/2t)
(e) 2 s e - /4 cos(π/2t+π)
Ver solução completaQuestão 31
Um bloco preso a uma extremidade de uma mola executa um movimento harmônico simples no eixo x. Os limites do movimento são x = 10 cm e x = 50 cm e o bloco vai de um limite ao outro em 0,25 s. A amplitude e a frequência do movimento são:
a) 20 cm e 2 Hz;
b) 40 cm e 2 Hz;
c) 40 cm e 4 Hz;
d) 25 cm e 4 Hz;
e) 20 cm e 4 Hz;
Ver solução completaQuestão 32
Considere um bloco de massa M preso a uma mola de constante elástica k. O bloco se encontra em repouso quando um objeto de massa m e velocidade v o atinge e se aloja no bloco. Após a colisão, a mola se alonga e o sistema realiza um movimento harmônico simples (MHS). Desprezando a compressão da mola durante a colisão e assumindo t = 0 o instante imediatamente após a colisão, marque a alternativa correta que descreve a solução x(t) do MHS resultante.
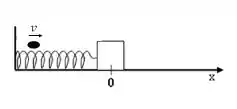
a)
b)
c)
d)
e)
f)
g)
h)
i)
Ver solução completaQuestão 33
Um carrinho (1) de massa M = 0,250 kg está preso à extremidade de uma mola realizando movimento harmônico simples com intervalos de tempo de 0,1 s entre dois extremos consecutivos de sua oscilação. No instante inicial, ele se move em direção à parede, passando pela posição x = 0 com velocidade v = 20 m/s 62,8 m/s.

a) Determine o período, a frequência, a frequência angular, a amplitude do movimento do carrinho(1) e a constante elástica da mola.
b) Escreva as expressões para o deslocamento e a velocidade do carrinho (1) em função do tempo, respectivamente x(t) e v(t).
c) Determine o instante de tempo em que o carrinho (1) passa pela extremidade à esquerda da oscilação pela primeira vez.
Ver solução completaQuestão 34
O bloco de massa está acoplado a uma mola de constante elástica como na figura. O bloco é deslocado para a direita sobre uma superfície perfeitamente lisa, esticando a mola de , e posteriormente é abandonado a partir do repouso. Qual das funções abaixo descreve o movimento oscilatório deste bloco sobre o eixo x, orientado para a direita, com origem na posição de equilíbrio do bloco?
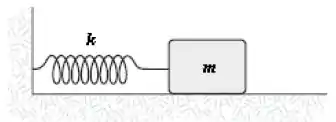
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 35
A figura mostra três osciladores harmônicos de mesma massa e constante elástica Não há atrito entre o bloco e as superfícies de contato, nem resistência do ar. Pode-se dizer das frequências angulares naturais de oscilação que
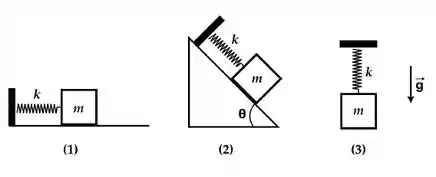
Questão 36
Um sistema massa-mola não amortecido é formado por um bloco de massa e por uma mola de constante elástica O sistema é submetido a uma força externa dada por
sendo
Sabendo que no instante , o bloco encontra-se em repouso, na posição , é correto afirmar que:
a)
b)
c)
d)
e) Nenhuma das demais alternativas.
Ver solução completaQuestão 37
Duas esferas uniformes estao picotadas sobre um eixo horizontal que passa pelo ponto O. Dado que o momento de inércia da esfera passando pelo seu centro podemos afirmar que a esfera com maior período de oscilação é aquela com:
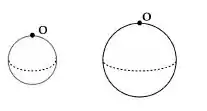
a) a maior massa.
b) o menor momento de inércia rotacional
c) a menor massa.
d) o maior raio.
e) o maior momento de inércia rotacional.
Ver solução completaQuestão 38
Considere o movimento harmônico simples de um bloco de massa ligado a uma parede vertical através de uma mola de constante elástica , como ilustrado na figura abaixo. Não há atrito entre o bloco e o plano horizontal e nem há resistência do ar neste ambiente. Sabe-se que no instante o bloco está na posição , onde a deformação da mola é máxima. Nestas circunstâncias, calcule:
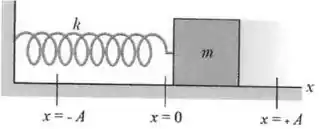
- O valor da constante de fase deste movimento harmônico simples.
- O instante de tempo para o qual a posição do bloco é .
- O instante de tempo para o qual a energia potencial elástica da mola é igual da energia mecânica do sistema em .
Questão 39
Um malabarista de está pendurado por uma corda com constante elástica de , que pode ser modelada como uma mola. Ele é puxado para baixo, até um ponto em que a corda está mais comprida do que seu comprimento não esticado, e depois é liberado a partir desta posição. Adotando o eixo mostrado na figura e considerando que as oscilações verticais do malabarista constituem um MHS unidimensional, a posição do malabarista como função do tempo, medida a partir da posição de equilíbrio do malabarista, é:
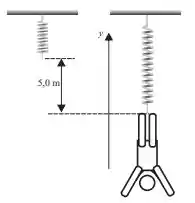
a)
b)
c)
d)
e)
Ver solução completaQuestão 40
Um oscilador consiste em um bloco de massa preso a uma dada mola. Ao oscilar com amplitude de ele repete seu movimento a cada . Suponha que a posição seja dada por . Se a posição do bloco em é a maior possível, determine:
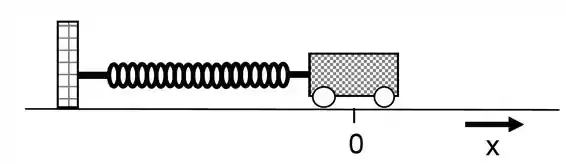
O período e a frequência angular do movimento;
A constante da mola;
A velocidade máxima e a energia mecânica do oscilador;
A constante de fase ;
Suponha agora que outro oscilador , idêntico ao primeiro e oscilando paralelamente a ele, seja liberado, em , a partir do repouso na posição .
Escreva as expressões e , das posições dos osciladores, e represente num mesmo gráfico essas funções para .
Encontre as duas posições em que eles se cruzam.
Ver solução completaQuestão 41
O gráfico mostra a posição em função do tempo de uma partícula de massa , ligada a uma mola de massa desprezível, que move-se em movimento retilíneo, sobre uma mesa horizontal lisa, na direção do eixo x, orientado para a direita.
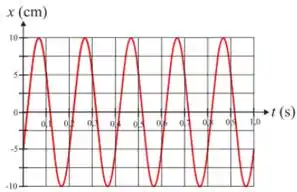
. Se o movimento realizado pela massa é um e a sua posição de equilíbrio ocorre em , podemos afirmar que a expressão da posição da partícula em função do tempo,
no sistema , é dada por:
Ver solução completaQuestão 42
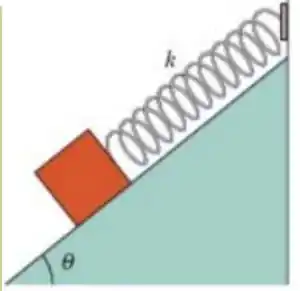
A figura ao lado mostra um bloco com de peso, que pode deslizar sem atrito em um plano inclinado de ângulo e está ligado ao alto do plano inclinado por uma mola, de massa desprezível, de de comprimento quando relaxada, cuja constante elástica é . A que distância do alto do plano inclinado fica o ponto de equilíbrio do bloco? Se o bloco é puxado ligeiramente para baixo ao longo do plano inclinado e depois liberado, qual é o período das oscilações resultantes?
Questão 43
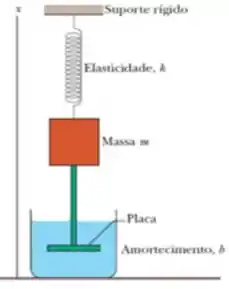
Em um oscilador amortecido como o que está mostrado na figura ao lado, o bloco possui uma massa de e a constante elástica é . A força de amortecimento é dada por , em que . O bloco é puxado para baixo e liberado. Calcule o tempo necessário para que a amplitude das oscilações resultantes diminua para um terço do valor inicial. Quantas oscilações o bloco realiza neste intervalo de tempo?
Questão 44
Um bloco de massa m está sobre outro bloco de massa M que executa um movimento harmônico simples sobre uma superfície horizontal sem atrito com frequência de 1,50 Hz. O coeficiente de atrito estático entre os dois blocos é 0,600. Qual a amplitude máxima de oscilação do sistema para m não deslizar sobre M ?
Ver solução completaQuestão 45
Considere uma caixa de madeira de massa , inicialmente em equilíbrio sobre uma superfície horizontal (sem atrito), ligada a uma mola ideal de constante presa a uma parede. No instante um projétil de massa e velocidade em módulo, se movendo na direção horizontal, atinge a caixa e fica preso a ela. Após isto, o sistema formado pela caixa e pelo projétil passa a oscilar harmonicamente. A frequência angular e a velocidade inicial do sistema são dadas, respectivamente, por
Escolha uma opção:
e
e
e
e
e
Ver solução completaQuestão 46
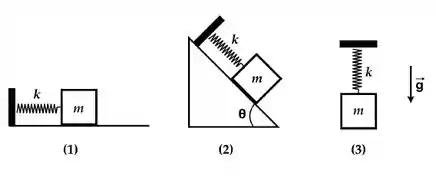
A figura mostra três osciladores harmônicos de mesma massa e constante elástica Não há atrito entre o bloco e as superfícies de contato, nem resistência do ar. Pode-se dizer das frequências angulares naturais de oscilação que
Questão 47
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A velocidade do bloco no instante que ele atinge a mola.
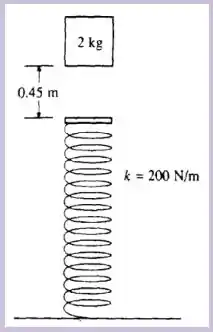
Questão 48
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A distância comprimida da mola na posição de equilíbrio.
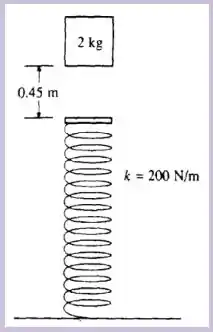
Questão 49
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
O período da oscilação.
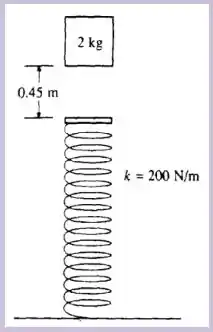
Questão 50
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A velocidade do bloco na posição de equilíbrio.
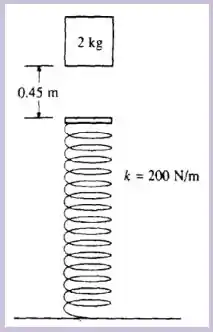
Questão 51
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A amplitude da oscilação resultante
Questão 52
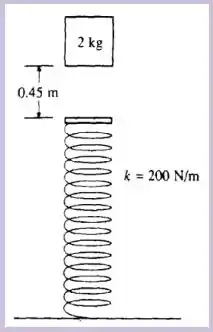
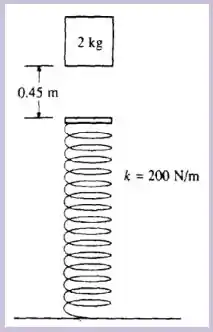
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
Pode-se afirmar que a velocidade do bloco na posição de equilíbrio corresponde a sua máxima? Explique
Questão 53
Um oscilador consiste num bloco preso a uma mola de constante elástica 456 N/m. Num dado instante o bloco passa pela posição 0,112 m, medida em relação a sua posição de equilíbrio, com velocidade de -13,6 m/s e aceleração de -123 m/. Calcule a massa do bloco, a frequência e a amplitude de oscilação.
Ver solução completaQuestão 54
Um bloco de massa m está sobre uma superfície horizontal e preso a uma mola ideal de constante elástica k. Outro bloco de massa M é encostado no bloco m, como mostra a figura, e empurrado de modo a comprimir a mola de X. Nesta posição, o sistema é abandonado do repouso e desliza sobre a superfície sem atrito. Dados: X = 10,0 cm e M = 3 kg.
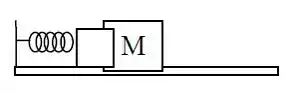
a) A partir de qual posição um bloco perderá o contato com o outro?
b) Qual a distância entre os blocos quando o bloco m atingir o repouso pela 2a vez após a perda de contato com M?
Ver solução completaQuestão 55
(Cap 13 - Ex 18) Uma massa de oscilador em uma mola tem a velocidade em função do tempo dada por . Qual é o período; a amplitude; a aceleração máxima da massa; a constante da mola?
Ver solução completaQuestão 56
Um bloco de massa M preso a uma mola de constante k descreve um movimento harmônico simples horizontal com uma amplitude . No instante em que o bloco passa pela posição de equilíbrio, um pedaço de massa m cai verticalmente sobre o bloco de uma pequena altura, grudando-se nele. A nova amplitude e período são:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 57
Uma partícula de massa m se move horizontalmente em um plano sem atrito, com velocidade v0 e atinge uma mola com constante elástica k. Ao atingir a mola, esta é comprimida e a partícula é ricocheteada com velocidade oposta. Assumindo que não existe nenhuma perda de energia, o tempo em que a partícula permanece em contato com a mola e a compressão máxima sofrida pela mola, são dados respectivamente por:
a) e
b) e
c) e
d) e
e) Nenhuma das alternativas.
Ver solução completaQuestão 58
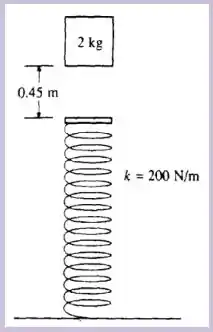
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A força na mola quando o bloco atinge a posição de equilíbrio.
Questão 59
A figura abaixo mostra os gráficos da energia cinética K em função da posição x para três osciladores harmônicos que têm a mesma massa. Ordene os gráficos de acordo com a constante elástica dos osciladores, começando pela maior.
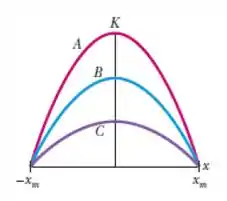
a) A, B, C;
b) B, A, C;
c) C, B, A;
d) A, C, B;
e) C, A, B;
Ver solução completaQuestão 61
No sistema massa-mola com mola de constante de elasticidade da figura, se a massa é substituída por , qual é o efeito sobre a posição de equilíbrio (medida ao longo do eixo e a partir da extremidade da mola relaxada) e sobre o período?
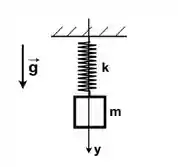
- A posição de equilíbrio será um fator menor e o período será um fator menor.
- A posição de equilíbrio será um fator 2 menor e o período será um fator menor.
- A posição de equilíbrio será um fator 2 maior e o período será um fator maior.
- A posição de equilíbrio será um fator menor e o período será um fator maior.
- A posição de equilíbrio será um fator menor e o período será um fator 2 maior.
Questão 62
O gráfico representa uma posição de uma massa ligada a mola. No instante indicado pela linha tracejada, qual afirmação é correta?
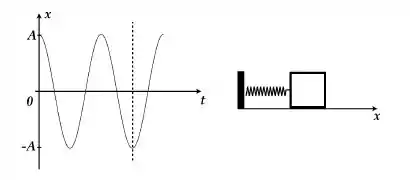
- a velocidade é nula e força restauradora para direita.
- a velocidade é negativa e força restauradora para esquerda.
- a velocidade é negativa e força restauradora para direita.
- a velocidade é positiva e força restauradora para direita.
- a velocidade é nula e força restauradora para esquerda.
Questão 63
Na figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
d. Qual seria a massa do disco para que a frequência fosse igual a do sistema simples massa-bloco ( com massa M e constante k).
Ver solução completaQuestão 64
Um objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
a. Determine a amplitude, a frequência, a frequência angular e o período desse movimento.
Ver solução completaQuestão 65
Um objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
b. Escreva a equação da velocidade do objeto.
Ver solução completaQuestão 66
Um objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
d. Qual o valor da constante-de-mola associada a esse movimento?
Ver solução completaQuestão 67
Na figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
c. Qual seria a constante elástica para que um sistema consistindo de uma mola e um bloco oscilasse com a mesma frequência que o sistema disco-mola?
Ver solução completaQuestão 68
Um objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
c. Escreva a equação da aceleração do objeto.
Ver solução completaQuestão 69
Um pêndulo é constituído por uma partícula de massa M pendurada na extremidade de uma barra rígida fina de massa desprezível e comprimento L. Uma mola de constante elástica k é conectada à barra a uma distância h abaixo do ponto de suspensão, conforme a figura abaixo. Encontre a frequência angular do sistema para valores pequenos da amplitude .
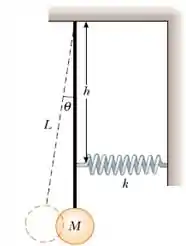
Questão 70
Quatro (4) molas de mesmo comprimento são comprimidas em relação à sua posição de equilíbrio como na figura. Qual resultado é satisfeito por suas velocidades máximas se as molas são liberadas a partir do repouso?
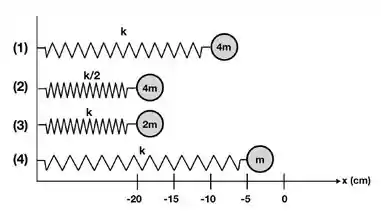
Questão 71
Um bloco está pendurado na extremidade de uma mola ideal. O bloco executa um movimento harmônico simples vertical de amplitude e período . Se a amplitude for o dobro, o período será:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 72
Um corpo oscila no plano horizontal ao longo de um eixo sob a ação de um força restauradora. Tome a origem das coordenadas no ponto onde a força restauradora é nula. Considera as seguintes situações, observadas em três tempos diferentes:
- e
- e
- e
Onde e são, respectivamente, a velocidade e a aceleração do corpo. Em quais situações a posição do corpo é positivo:
- Somente
- Somente
- Somente
- Somente e .
- Somente e
Questão 73
Um carro de com quatro ocupantes de viaja em uma estrada de terra com “costelas” separadas por uma distância média de . O carro trepida com amplitude máxima quando está a . Quando o carro para e os ocupantes saltam, qual é a variação de altura do carro?
a)
b)
c)
d)
e) Nenhuma das demais alternativas
Ver solução completaQuestão 74
A extremidade de uma mola oscila com um período de quando um bloco, de massa , está preso à mola. Quando a massa é aumentada de , o período do movimento passa a ser . Determine o valor de .
Ver solução completaQuestão 75
(Cap 13 - Ex 8) Quando uma massa de 0,750 kg oscila em uma mola ideal, a frequência é igual a 1,33 Hz. Qual será a frequência se 0,220 kg forem adicionados à massa original, e (b) subtraídos à massa original? Tente resolver este problema sem achar a constante da mola.
Ver solução completaQuestão 76
Um corpo de 0,500 kg oscila preso a uma mola ideal. A velocidade do corpo é dada pela função:
Para t em s e V em cm/s. Determine:
a) o período;
b) a amplitude;
c) a aceleração máxima;
d) a constante elástica da mola.
Ver solução completaQuestão 77
Um bloco de 0,400 kg está em repouso, pendurado numa mola ideal de constante elástica 78,4 N/m. O bloco é levantado desta posição até uma posição situada 15,0 cm acima e abandonado a partir do repouso.
a) Qual a amplitude de oscilação?
b) Qual a força elástica e a força resultante em cada ponto extremo da trajetória do bloco?
c) Qual o período de oscilação?
d) Qual a velocidade máxima do bloco?
Ver solução completaQuestão 78
Uma mola tem uma extremidade fixada numa parede e a outra num carrinho, que pode movimentar-se numa superfície horizontal sem atrito. O carrinho me movimento comporta-se como um oscilador harmônico realizando um movimento harmônico simples. Se o carrinho realiza ciclos/s e no instante inicial de movimento encontra-se na posição com velocidade , a amplitude da oscilação é:
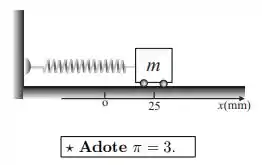
a)
b)
c)
d)
e)
Ver solução completaQuestão 79
Uma forma de medir a massa m de um objeto em uma estação espacial é suspendê-la por um sistema elástico. Primeiramente o astronauta mede a frequência de oscilação do sistema elástico com uma massa conhecida. Depois, a massa (desconhecida) é adicionada ao sistema e uma nova medida de frequência, , de oscilação é tomada. Qual o valor da massa em função dos dois valores de frequência medidos?
(a)
(b) .
(c) .
(d) .
(e) Como não há gravidade, enão é possível determinar .
(f) Nenhuma das respostas anteriores.
Ver solução completaQuestão 80
As missões Apollo 15, 16 e 17 levaram um jipe para a superfície lunar. Esse jipe quando totalmente carregado possui uma massa , a mola da suspensão possui uma frequência natural de oscilação de medidos na superfície terrestre. Sabendo que a aceleração da gravidade na superfície lunar equivale a ao da aceleração na superfície terrestre, pode-se afirmar que a frequência natural da oscilação da suspensão do jipe na superfície lunar é
- Depende da massa do jipe,
Questão 82
Um bloco de massa está preso à extremidade inferior de uma mola ideal de constante elástica cujo extremo superior está preso ao teto por um suporte fixo e alinhada com a direção vertical. Um segundo bloco, também de massa , está ligado ao primeiro bloco por meio de um fio ideal. Inicialmente, o sistema encontra-se em equilíbrio, como mostra a figura.
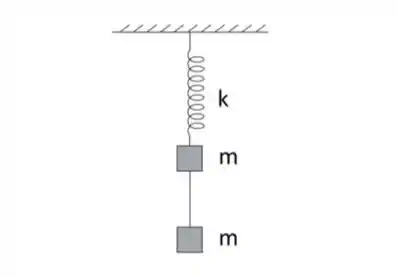
Em um dado instante, corta-se o fio e o sistema formado pela mola e pelo bloco preso em sua extremidade inferior começam a oscilar verticalmente. Supondo desprezíveis todos os atritos e sendo o módulo da aceleração da gravidade, assinale a opção que indica, respectivamente, o período e a amplitude das oscilações harmônicas executadas por esse bloco.
(a) e .
(b) e .
(c) e .
(d) e .
(e) e .
Ver solução completaQuestão 83
Considere um pêndulo constituído de uma mola com uma massa presa na sua extremidade, conforme mostrado na Figura . A mola é disposta de tal forma que fica em linha reta (por exemplo, podemos imaginar que existe uma barra rígida envolvida pela mola). O comprimento da mola é . A mola é então esticada de um comprimento , passando a assumir um comprimento . Ao mesmo tempo, o pêndulo é deslocado de um ângulo com a vertical. Com base nessas informações, considere as alternativas a seguir.
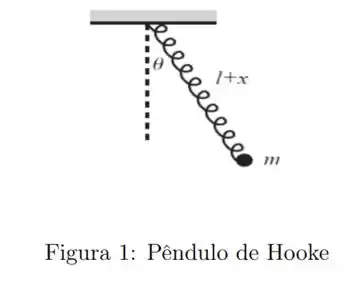
Mostre que a lagrangeana correspondente ao sistema dado é
Ver solução completaQuestão 84
Considere um pêndulo constituído de uma mola com uma massa presa na sua extremidade, conforme mostrado na Figura . A mola é disposta de tal forma que fica em linha reta (por exemplo, podemos imaginar que existe uma barra rígida envolvida pela mola). O comprimento da mola é . A mola é então esticada de um comprimento , passando a assumir um comprimento . Ao mesmo tempo, o pêndulo é deslocado de um ângulo com a vertical. Com base nessas informações, considere as alternativas a seguir.
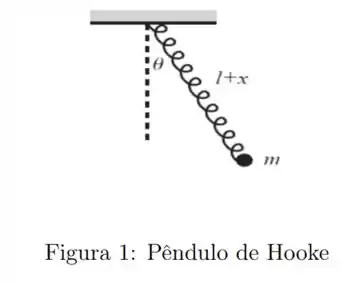
Obtenha as equações de movimento relativas às coordenadas e .
Ver solução completaQuestão 85
Um famoso problema no cálculo das variações é o seguinte: dado dois pontos e , com a uma certa altura acima do solo, qual será a forma que devemos construir os trilhos de uma montanha-russa, sem atrito, de modo que um carro largado do ponto alcance ponto no menor tempo possível? (Esse é o famoso problema da braquistócrona, resolva-o em detalhe).
Ver solução completaQuestão 86
Um bloco de 175 g preso a uma mola ideal de constante elástica 155 N/m executa um movimento harmônico simples sobre um trilho de ar horizontal. Num dado instante o corpo passa a 3,00 cm da posição de equilíbrio com velocidade de 0,815 m/s. Determine a amplitude, o período e a velocidade máxima do corpo.
Ver solução completa