Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 50
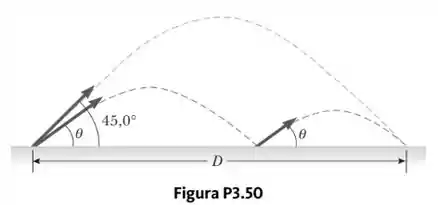
Um jogador de beisebol lança uma bola para o recebedor do seu time em uma tentativa de jogar um corredor para fora da base. A bola ricocheteia uma vez antes de chegar ao recebedor. Assuma que o ângulo no qual a bola sai do chão é o mesmo com que o jogador lançou a bola, como mostrado na Figura P3.50, mas que a velocidade da bola após o salto é metade do que era antes do salto.
Assuma que a bola é lançada sempre com a mesma velocidade inicial e ignore a resistência do ar. Em que ângulo o jogador deveria jogar a bola para que ela percorresse a mesma distância D com um ricochete (trajetória pontilhada inferior) como uma bola jogada para cima a 45,0° sem ricocheteio (trajetória pontilhada superior)?
Determine a relação entre o intervalo de tempo para o lançamento com um ricocheteio e o tempo de voo para o lançamento sem ricochete.
Passo 1
Amores, vamos começar escrevendo uma equação envolvendo a distância a partir da velocidade de deslocamento horizontal da bola, que é sempre constante, por ser um movimento uniforme.
A gente pode escrever isso aqui:
Onde é a velocidade de deslocamento horizontal e é o tempo de deslocamento.
Só que a gente sabe de exercícios anteriores que podemos escrever melhor assim, a partir do esqueminha a seguir:
Logo, , em que é a velocidade original de lançamento da bola, beleza? Mas como nesse caso , a gente tem que
Chegamos então à expressão melhorada:
Guarda isso que já já a gente vai fazer uso!
Passo 2
Ok, agora a gente vai analisar o lançamento com ricocheteio, separando em 2 momentos: antes do ricocheteio e depois do ricocheteio, ok?
Pro momento antes do ricocheteio, avaliando o deslocamento horizontal, a gente pode escrever o seguinte:
Onde , e são respectivamente a velocidade horizontal de deslocamento da bola, a distância horizontal alcançada no ricocheteio e o tempo que levou até o ricocheteio, ok?
Mas como a gente fez no Passo 1, dá pra gente reescrever assim:
Onde é a velocidade original de lançamento pra esse caso.
Então, melhoramos a nossa expressão assim:
Passo 3
Fazemos o mesmo pra depois do ricocheteio, de modo análogo, a gente tem:
E. melhorando, podemos ainda escrever assim
Só queee, no enunciado a gente viu que a velocidade original pós ricocheteio é metade da velocidade original do lançamento inicial! Ou seja:
E, além disso, vale dizer que a soma das distâncias e equivale a , além de que os tempos e , somados, precisam também valer o tempo do lançamento a , uma vez que alcançam a mesma posição final. Matematicamente, escrevemos:
E
Passo 4
Do Passo 1, a gente obteve uma relação pra . Vamos reescrever ela a partir do que a gente obteve agora no último Passo. Vale o seguinte:
Certinho?
Só que a gente pode reescrever do seguinte modo, ainda, usando as expressões pras velocidades dos Passos 2 e 3, isolando-se e :
Lembrando que , a gente melhora isso mais ainda, assim:
Vamos colocar o que for possível em evidência, assim:
E agora, gente, lembra que a velocidade original de lançamento foi igual pros dois casos, portanto, ! E dá pra gente cortar os termos em cima e embaixo! Beleza, vamos simplificar isso ainda mais, chegando nisso aqui:
E, com isso, temos:
Assim, o ângulo deve valer .
E como a gente discutiu, em relação aos tempos de voo, no total, eles precisam ser os mesmos pra que a bola alcance a mesma distância D, tudo bem?