Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 15.Exercícios e Problemas - Ex. 14
15.14E Um disco de raio igual a está carregado com uma densidade de carga uniforme . Calcule o campo elétrico a distância de do disco em um ponto sobre seu eixo.
Passo 1
Belezera meus amores, como estamos tratando de medir o campo de um disco plano com carga uniformemente distribuída à distância de um ponto, podemos representar esse desenho como:
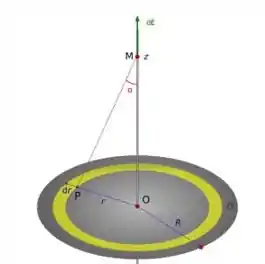
Onde nosso ponto no eixo representa o ponto que desejamos medir o campo elétrico. Usando o método dos anéis do disco, chegamos na fórmula que nos devolve o campo de um disco, dada como:
Passo 2
Show de bolinhas, e o enunciado já nos deu que , que o raio do disco é e além disso a distância no ponto até o disco é dada por . E passando todas as unidades de para , teremos que:
Resposta
Exercícios de Livros Relacionados
15.1E Calcule a força entre duas cargas de um coulomb afastadas uma da outra um quilômetro.
15.3E Calcule a força de repulsão entre dois prótons dentro de um núcleo, distantes um do outro 1,5 × 10 - 15 m .
15.9E Duas partículas de mesma carga q estão separadas por uma distância fixa. Queremos introduzir uma terceira partícula carregada ao conjunto, deforma que todas as partículas sintam força resultante
15.2E Considere um elétron orbitando em torno de um próton, em uma órbita de raio igual a 0,051nm . Calcule a força de atração elétrica entre essas partículas e compare o resultado com a força de atra
15.5E As três esferas vistas na Figura 15.14 têm diâmetro muito menor do que as distancias entre elas. Calcule a relação x / L para que a força sobre a esfera azul seja nula.