Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 73
Como dissemos no Exercício 1.26, uma pesquisadora está estudando uma caverna. Ela percorre 180 m em linha reta de leste para oeste, depois caminha 210 m em uma direção que forma 45° com a direção anterior e em sentido do sul para o leste, a seguir percorre 280 m a 30° no sentido do norte para o leste. Depois de um quarto deslocamento não medido, ela retorna ao ponto de partida. Use o método dos componentes para determinar o módulo, a direção e o sentido do quarto deslocamento. Verifique se a solução obtida usando-se um diagrama em escala é aproximadamente igual ao resultado obtido pelo método dos componentes.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma pesquisadora faz os seguintes passos em uma caverna:
- Ela percorre em linha reta de leste para oeste;
- depois caminha em uma direção que forma com a direção anterior e em sentido do sul para o leste;
- percorre a no sentido do norte para o leste;
- depois de um quarto deslocamento não medido, ela retorna ao ponto de partida.
Queremos determinar o módulo, a direção e o sentido do quarto deslocamento.
Para isso, devemos desenhar em um plano cartesiano os passos (em forma de vetores) para podermos resolver isso.
Passo 2
Desenhando os passos, temos:
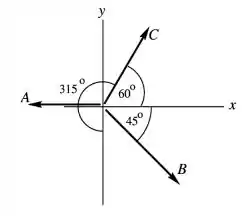
Como a pesquisadora quer voltar ao ponto de partida, isso quer dizer que a soma dos deslocamentos é igual a .
Então a gente só precisa achar as componentes do quarto vetor () pra que a soma dos deslocamentos em e em dê igual a .
Daí, usamos Pitágoras para achar o módulo. Olha que simples!
Então vem com a gente!
Passo 3
Primeiro vamos achar os valores de e . Começando por x:
Agora em :
Passo 4
Agora usamos Pitágoras pra achar o módulo de .
Achamos o módulo!! \O/ Agora é só achar o ângulo com o eixo -Ox.
Passo 5
Pra achar o ângulo com o eixo -Ox vamos usar o método da tangente.
Agora usamos o arco-tangente para descobrir o ângulo e já era:
Terminamos mais uma!!!!
Passo 6
Agora desenhamos o diagrama:
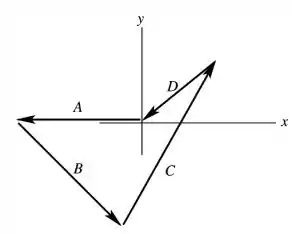
E a solução é realmente parecida com os dados que encontramos.
Conseguimos mais uma vez, pimpolhos!
Resposta
Módulo:
Direção: com o eixo