Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 68
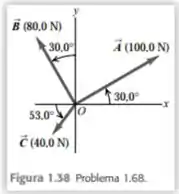
Três cordas horizontais puxam uma pedra enorme encravada no solo, produzindo as forças vetoriais , demonstradas na Figura 1.38. Encontre o módulo e a direção de uma quarta força que produzirá a soma vetorial zero para as quatro forças.
Passo 1
Fala aí! Tudo certinho?
Bora lá! A questão tá dizendo que tem três cordas horizontais puxando uma pedra enorme que tá cravada no solo. Elas serem horizontais quer dizer que ninguém vai puxar pro céu e nem de volta pro chão. Haha. Aí a figura dá a direção e a intensidade dessas forças e o que ela quer saber é a intensidade e a direção de uma corda pra que a soma das forças dê zero.
Então a gente quer saber o valor de pra que e pra isso a gente vai ter que decompor os vetores em suas componentes. Depois queremos saber qual a direção desse vetor, pra isso a gente vai ter que encontrar o ângulo dele e o sentido.
Ainda não descobriu como fazer? Então vem com a gente, jovem padauã!
Passo 2
Primeiro decompomos os vetores em relação ao eixo x. Pra isso a gente vai multiplicar o módulo, ou seja, a intensidade de cada vetor pelo cosseno do ângulo que ele faz com o eixo x, caso o ângulo esteja no eixo x, ou pelo seno do ângulo que ele faz com o eixo y, caso o ângulo esteja no eixo y.
Um lembrete é de que, quando o vetor está apontado pro lado negativo do eixo, a intensidade dele fica negativa.
Vamo ver como vai ficar isso: XD
Tranquilo até aqui?
Passo 3
Agora vamos decompor em relação ao eixo y:
Bacana, não é?
Passo 4
Agora que decompomos os vetores, vamos somar as componentes em x com a componente x da corda e igualar tudo a zero, assim vamos descobrir qual deve ser a intensidade da força da corda em x pra que a soma das forças em x seja igual a 0. Então bora lá:
Estamos quase lá!
Passo 5
Agora a gente vai fazer o mesmo pro eixo y:
Legal, né?
Passo 6
Agora a gente tem a intensidade em do vetor em x e em y. Mas como saber o verdadeiro módulo dessa força? Vamos usar o teorema de Pitágoras que mostra que .
Então nós vamos ter:
Aeh! Achamos a intensidade da força da corda D, agora só falta encontrar o ângulo e a posição dessa corda.
Passo 7
Pra encontrar o ângulo que essa corda faz com o eixo x é só usar a expressão da tangente: . Então teremos:
Agora fazemos e achamos um ângulo de em relação ao eixo x.
E pra saber a posição da corda é só ver que os valores dela tanto em x quanto em y são negativos. Portanto, a corda está no terceiro quadrante.
Olha a imagenzinha aí ilustrando:
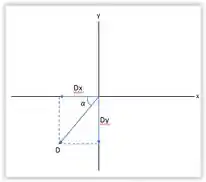
E finalizamos mais uma questão. YES!
Entendeu tudo? Responde Aí!
Resposta
Módulo de situada no terceiro quadrante, fazendo ângulo de como eixo x.