- Qual é o ângulo entre os vetores e da FIGURA P3.26?
- Use geometria e trigonometria para determinar o módulo e a orientação de .
- Use os componentes para determinar o módulo e a orientação de .
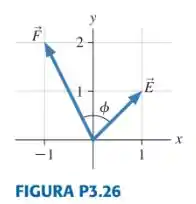
Passo 1
- Qual é o ângulo entre os vetores e da FIGURA P3.26?
- Use geometria e trigonometria para determinar o módulo e a orientação de .
- Use os componentes para determinar o módulo e a orientação de .
Vamos olhar a figura e achar as componentes e de cada vetor:
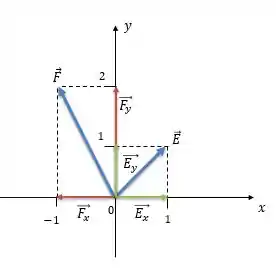
Para :
Para :
Passo 2
Agora vamos achar o ângulo que cada vetor faz com o semi-eixo positivo:
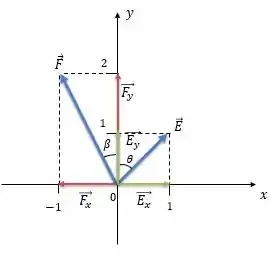
Para isso, vamos fazer o seguinte:
E:
Mas não são esses dois ângulos que queremos né, queremos o ângulo entre os dois vetores:
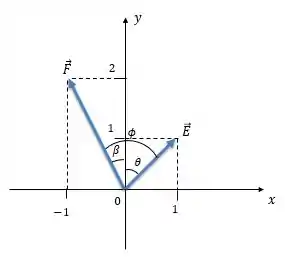
Passo 3
Vamos fazer a soma gráfica:
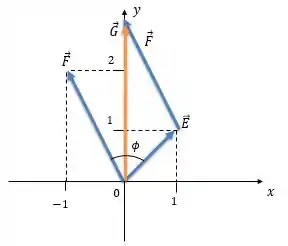
Para calcular o módulo vamos utilizar a lei dos cossenos:
já calculamos, então:
Precisamos calcular o módulo de e :
Retornando a lei dos cossenos:
Passo 4
Agora para determinar a orientação, vamos achar o ângulo que o vetor faz com o eixo :
Olha a imagem:
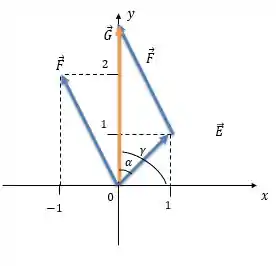
Já conhecemos quem é o ângulo , calculamos lá no passo 2:
Se o vetor faz com o eixo , ele também faz com o eixo , porque como os dois eixos são perpendiculares, a soma entra esses dois ângulos tem que ser . E note que é exatamente a soma entre esses dois ângulos, então:
Passo 5
Como é a soma entre os vetores e , as componentes de também serão a soma das componentes de e :
Agora para calcular o módulo vamos fazer:
Passo 2
Agora, para acharmos a orientação precisamos achar o valor do ângulo que o vetor faz com o eixo .
Vimos que a componente desse vetor é zero, isso quer dizer que ele está na direção do eixo e consequentemente o ângulo que ele faz com o eixo é . Podemos ver isso na imagem:
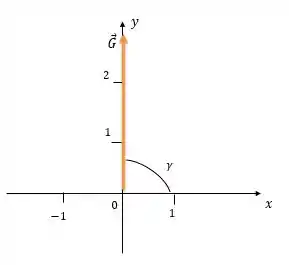
O vetor tem módulo igual a e faz com o eixo .
Resposta
- e faz com o eixo .
- O vetor tem módulo igual a e faz com o eixo .