Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 10.Problemas - Ex. 1

Em 1968 , a nave espacial Apolo 8 foi colocada numa órbita circular em torno da Lua, a uma altitude de 113   k m acima da superfície. O período observado dessa orbita foi de 1 h 59 m i n . Sabendo que o raio da Lua é de 1738   k m , utilize esses dados para calcular a massa da Lua.

Passo 1

Bora lá galera! Bem, vamos imaginar a situação no plano. Lua esférica, órbita circular, etc. Considerando então R como o raio da lua e h a altura de órbita acima da superfície, no plano, temos o seguinte:

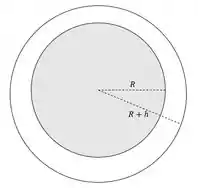
A distância então de Apolo 8 até o centro da lua é de:

R A P 8 = R + h

R A P 8 = 1738 + 113

R A P 8 = 1851   k m

R A P 8 ≅ 1 , 85 ∙ 10 6   m

Portanto, podemos reduzir o problema a um movimento circular de raior igual a R A P 8 , conforme a figura abaixo:

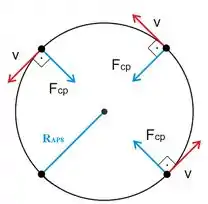
E vamos partir daqui, beleza?

Passo 2

Galera, a questão pede a massa da lua! Bom, se considerarmos todas as forças atuando vemos que na verdade, a única que atua é a centrípeta:

F C P = m A P 8 ∙ v A P 8 2 R A P 8

Só que veja bem, essa é uma questão sobre órbitas! Então existe uma força gravitacional também a se considerar:

F G = G ∙ m L u a ∙ m A P 8 R A P 8 2

A verdade é que essas forças vão ser iguais! Então vamos ter:

G ∙ m L u a ∙ m A P 8 R A P 8 2 = m A P 8 ∙ v A P 8 2 R A P 8

Isolando a massa da lua, que é o que queremos encontrar:

m L u a = m A P 8 ∙ v A P 8 2 ∙ R A P 8 2 R A P 8 ∙ G ∙ m A P 8

m L u a = v A P 8 2 ∙ R A P 8 G

Substituindo o que sabemos:

m L u a = v A P 8 2 ∙ 1,85 ∙ 10 6   m 6 , 67 ∙ 10 - 11     m 3 k g ∙ s 2

m L u a ≅ v A P 8 2 ∙ 2,77 ∙ 10 16   k g ∙ s 2 m 2

E agora vamos conversar sobre como achar a velocidade

Passo 3

Vamos olhar pro dado do enunciado que a gente não usou ainda: “O período observado dessa orbita foi de 1 h 59 m i n .”. Sendo uma órbita o mesmo que uma volta inteira no círculo, podemos dizer que a velocidade é o número de voltas sobre o tempo:

v A P 8 = 1   v o l t a 1 h   59 m i n

Só que bem, essa unidade de medida ta meio ruim. Vamos por ela no S I . Como uma volta inteira, em metros, seria o equivalente ao tamanho da circunferência de órbita, substituímos por:

v A P 8 = 2 ∙ π ∙ R A P 8     m e t r o s 1 h   59 m i n

E no S I , devemos usar segundos! Vamos ter então:

1 h   59 m i n = 1 h + 59 m i n = 60   m i n + 59 m i n = 119   m i n

Como em um minuto temos 60 segundos:

119   m i n = 119 ∙ 60   s e g u n d o s

E tai! A velocidade em S I é:

v A P 8 = 2 ∙ π ∙ R A P 8     m e t r o s 119 ∙ 60   s e g u n d o s

v A P 8 = 2 ∙ π ∙ R A P 8 119 ∙ 60       m / s

v A P 8 = 2 ∙ π ∙ 1,85 ∙ 10 6 119 ∙ 60       m / s

v A P 8 ≅ 1,63   ∙ 10 3     m / s

Substituindo na fórmula da massa da lua que achamos no passo anterior:

m L u a ≅ v A P 8 2 ∙ 2,77 ∙ 10 16   k g ∙ s 2 m 2

m L u a ≅ 1,63   ∙ 10 3     m / s 2 ∙ 2,77 ∙ 10 16   k g ∙ s 2 m 2

m L u a ≅ 2,66   ∙ 10 6   m 2 s 2 ∙ 2,77 ∙ 10 16   k g ∙ s 2 m 2

m L u a ≅ 7,37   ∙ 10 22       k g

Resposta

m L u a ≅ 7,37   ∙ 10 22       k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8 . | Qual é a aceleração de queda livre na superfície ( a ) da Lua e ( b ) de Júpiter?
11 . || O Planeta Z tem 10.000k m de diâmetro, e a aceleração de queda livre nele é de 8m / s 2 a. Qual é a massa do Planeta Z?b. Qual é a aceleração de queda livre em uma posição 10.000k m acima do p
2 . A força gravitacional de uma estrela sobre o planeta na órbita 1 é F 1 . O planeta 2 , que tem massa duas vezes maior do que a do planeta 1 e orbita a uma distância duas vezes maior, experimenta u
1. A força gravitacional da Terra sobre o Sol é maior, menor ou igual à força gravitacional do Sol sobre a Terra? Explique.
Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve: a. Redigir um problema realista para o qual esta seja a equação correta. b. Fa