Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 10.Problemas - Ex. 17

Um fio homogêneo de massa M tem a forma de um anel circular de raio a . Calcule a força de atração gravitacional exercida pelo fio sobre uma partícula de massa m situada sobre o eixo (perpendicular ao plano do anel que passa pelo seu centro), à distância D do centro do anel.

Passo 1

Aqui, a gente vai considerar um pedaço bem pequeno do anel com comprimento d l . Vamos chamar de λ a densidade linear de massa dele, daí:

d m = λ d L

λ = M 2 π a

Agora vamos equacionar o campo gravitacional. Olha essa ilustração aqui embaixo:

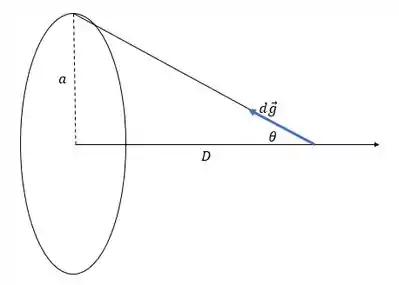
Para acharmos a distância entre nosso pedaço de anel e o eixo, vamos lembrar do nosso amigo Pitágoras!

d 2 = a 2 + D 2

Nosso campo vai ficar assim:

d F = G d m a 2 + D 2

Como d m = λ d L :

d F = G λ d L a 2 + D 2

Passo 2

Olha ali pro desenho. Tá vendo que as componentes verticais de d g → se anulam? Isso porque a distribuição é simétrica, ou seja, pra cada pedacinho, existe um diametralmente oposto que vai anular sua componente vertical!

No eixo x :

d F = d g ⋅ cos ⁡ θ = G λ d L a 2 + D 2 cos ⁡ θ

Da figura,

cos ⁡ θ = D a 2 + D 2

Logo,

d F = G λ d L a 2 + D 2 ⋅ a a 2 + D 2 = G λ D d L ( a 2 + D 2 ) 3 / 2

Como λ = M 2 π R :

d F = G λ D d L a 2 + D 2 3 / 2 = G M D d L 2 π a a 2 + D 2 3 / 2

Agora vamos integrar para achar o campo.

F = ∫ 0 2 π a G M m D 2 π a a 2 + D 2 3 / 2 d L

Botando pra fora o que é constante:

F = G M m D 2 π a a 2 + D 2 3 / 2 ⋅ ∫ 0 2 π a d L = G M m D 2 π a a 2 + D 2 3 / 2 ⋅ 2 π D

Portanto,

F = G M m D a 2 + D 2 3 2

Resposta

Por fim, a atração gravitacional entre o anel e a partícula é dada como :

F = G M m D a 2 + D 2 3 2 ( 0,0 , 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 13-39, uma partícula de massa m 1 = 0,67 k g está a uma distância de 23 cm de uma das extremidades de uma barra homogênea de comprimento L = 3,0 m e massa M = 5,0 k g . Qual é o módulo da forç
Um furo é feito da superfície da Terra até o seu centro, como na figura 11-30. Ignore a rotação da terra e a resistência do ar, e trate a Terra como uma esfera homogênea. (a) Qual é o trabalho necessá
Planetas não são uniformes por dentro. Normalmente eles são mais densos no nucelo e sua densidade vai descrevendo de dentro para fora té a superfície. Modele um planeta esfericamente simétrico, de mes
Um corpo com forma de anel fino possui raio a e massa M . Uma esfera uniforme de raio R e massa m é colocada com seu centro situado a uma distancia x à direita do centro do anel, sobre a linha que une
Uma barra uniforme deslgada possui comprimento L e massa M . Calcule o modulo da força gravitacional que a barra exerce sobre uma partícula de massa m situada ao longo do eixo da barra a uma distancia