Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 10

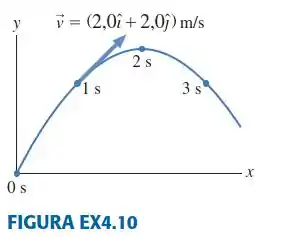
10 . | Um estudante de física no planeta Exidor arremessa uma bola, e ela segue a trajetória parabólica mostrada na F I G U R A   E X 4.10 . A posição da bola é mostrada em intervalos de 1 s até t   =   3 s . Em t = 1 s , a velocidade da bola é v → = ( 2 i ^ + 2 j ^ ) m / s .

a . Determine a velocidade da bola em t   =   0 s ,   2 s   e   3 s .

b . Qual é o valor de g na superfície do planeta Exidor?

c . Qual foi o ângulo de lançamento da bola?

Passo 1

a . Determine a velocidade da bola em t   =   0 s ,     2 s   e   3 s .

Esse tipo de lançamento, é chamado lançamento obliquo ele tem algmas caracteristcas, vamos falando conforme for necessário...

Lembre-se que sempre vamos decompor em uma componente x e um componente y .

Vamos primeiro analisar o que acontece de 1 s até 2 s

Já sabemos que em 1 s :

v → = ( 2 ⏞ v 1 x i ^ + 2 ⏞ v 1 y j ^ ) m / s

Como em 2 s a bola está no seu ponto mais alto, nesse instante perfeitamente paralela ao eixo x , ela não vai ter nenhum componente em y . Assim em 2 s sabemos que :

v y = 0 j ^   m / s

Nesse intervalo ( 1 s até 2 s ), podemos então aplicar uma das fórmulas da cinemática:

v = v 0   + a t

Para o componente y nesse intervalo ( 1 s até 2 s ):

v 2 y = v 1 y   + a t

0 = 2 m / s   + a ( 2 s - 1 s )

0 = 2 m / s   + a ( 1 s )

⇒   a = - 2 m / s 2

Agora que temos a aceleração, podemos evoluir, mas guarde essa informação.

Passo 2

Uma coisa importante é saber que nesse tipo de trajetória o componente x da velocidade em qualquer ponto é igual, isso quer dizer que a velocidade horizontal é constante no movimento do projétil, e nesse caso v x   =   2,0   m / s em todos os momentos. Ou em outras palavras, a velocidade horizontal é nula.

Em resumo numa trajetória obliqua:

  • Velocidade na horizontal é constante.
  • Velocidade na horizontal não existe aceleração.

Passo 3

Agora unindo a informação do p a s s o   1 com a informação do p a s s o   2 , temos que a bola tem aceleração - 2 m / s 2 , ou seja vai perdendo 2 m a cada quadrado de segundo, mas isso só irá acontecer no componente vertical, pois no horizontal a velocidade é constante e nem possui aceleração.Então ficamos com:

Em   t   =   0 s :

v →     =   ( 2.0 i ^       +   4.0 j ^ )   m / s  

Em   t   =   1 s   :

v →     =   ( 2.0 i ^       +   2 . 0 j ^ )   m / s  

Em   t   =   2 s   :

v →     =   ( 2.0 i ^       +   0 j ^ )   m / s  

Em   t   =   3 s   :

v →     =   ( 2.0 i ^     -   2 . 0 j ^ )   m / s  

Veja que v y começa com 4 para poder ser 2 no momento t = 1 , como a questão afirma!

Passo 4

b . Qual é o valor de g na superfície do planeta Exidor?

Sabemos que

a = a y = - 2,0 m / s 2  

Mas quando o movimento está agindo no sentido do centro da terra (chão),ou seja, quando estiver descendo, o sinal da gravidade é positivo, então:

g =   - a y

g =   - ( - 2,0 m / s 2 )

g = 2,0 m / s 2

Passo 5

c . Qual foi o ângulo de lançamento da bola?

Essa é fácil, basta usar trigonometria para velocidade em t = 0 s

Chegamos há:

θ = tan - 1 ⁡ v 0 y v 0 x

θ = tan - 1 ⁡ 4 m / s 2 m / s

θ = 63.4 °   a n t i - h o r a r i o + x

Resposta

( a )

Em   t   =   0 s :

v →     =   ( 2.0 i ^       +   4.0 j ^ )   m / s  

Em   t   =   2 s   :

v →     =   ( 2.0 i ^       +   0 j ^ )   m / s  

Em   t   =   3 s   :

v →     =   ( 2.0 i ^     -   2 . 0 j ^ )   m / s  

b

g = 2,0 m / s 2

( c )

θ = 63.4 °   a n t i - h o r a r i o + x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Num jogo de vôlei, desde uma distância de 14,5 m da rede, é dado um saque do tipo “jornada das estrelas”. A bola sobe a 20 m acima da altura de lançamento, e desce até a altura do lançamento num ponto
Viajando na traseira de um caminhão aberto, que está acelerando uniformemente com aceleração a = 3m / s 2 , numa estrada horizontal, um estudante preguiçoso resolve aplicar seus conhecimentos de físic
No exemplo 4-7b uma bala é disparada por um canhão situado ao nível do mar com um ângulo de 45 ° com a horizontal e atinge uma distância de 686m . Qual seria o aumento da distância atingida pela bala
Uma surpresa gráfica. No instante t = 0 , um burrito é lançado a partir de um terreno plano, com uma velocidade inicial de 16,0m / s e um ângulo de lançamento θ 0 . Imagine um vetor posição r → que li
O piloto de um avião voa para leste em relação ao solo enquanto um vento sopra a 20k m / h na direção sul. Se a velocidade do avião na ausência de vento é 70k m / h , qual é a velocidade do avião em r