Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 73

21.73 Duas cargas puntiformes positivas Q são mantidas fixas sobre o eixo O x , nos pontos x = a   e   x = - a . Uma terceira carga puntiforme positiva q, com massa m, é colocada sobre o eixo O x afastada da origem em um ponto x tal que | x |   < <   a . A carga q , que pode se mover livremente ao longo do eixo O x , é, a seguir, liberada. ( a ) Determine a freqüência das oscilações da carga q . (Sugestão: faça uma revisão da definição de movimento harmônico simples na S e ç ã o   13.2 . Use a série binomial 1   +   z n   =   1   +   n z   + n n   - 1 z 2 2 + … , válida para | z |     < < 1 . ( b ) Agora, suponha que a carga q seja colocada sobre o eixo O y em um ponto y tal que | y | < < a e, a seguir, liberada. Caso essa carga possa se mover livremente no plano x y , o que ocorrerá com ela?Explique sua resposta.

Passo 1

( a )

Sabendo:

F = - k x

f = 1 2 π ⋅ k m

Em q :

F x = F 1 x + F 2 x

F 1 x = + F 1     &     F 2 x = - F 2

F 1 = 1 4 π ϵ 0 ⋅ q Q a + x 2       &     F 2 = 1 4 π ϵ 0 ⋅ q Q a - x 2  

F x = 1 4 π ϵ 0 ⋅ q Q a + x 2     - 1 4 π ϵ 0 ⋅ q Q a - x 2

F x = q Q 4 π ϵ 0   1 a - x 2 - 1 a - x 2

F x = q Q 4 π ϵ 0 a 2   + 1 + x a - 2 - 1 - x a - 2

⇒ F = q Q 4 π ϵ 0 a 2   + 1 + x a - 2 - 1 - x a - 2

Passo 2

Fazendo x < < a , e olhando os denominadores, usamos a expansão binominal:

1 + z n ≅ 1 + n z  

Para

1 + x a - 2

z = + x a   e     n = - 2

⇒ 1 + x a - 2 ≅   1 - 2 x a

Para

1 - x a - 2

z = - x a   e     n = - 2

⇒ 1 - x a - 2 ≅   1 + 2 x a  

Passo 3

Reescrevendo:

F = q Q 4 π ϵ 0 a 2   + 1 + x a - 2 - 1 - x a - 2

F = q Q 4 π ϵ 0 a 2   1 - 2 x a - 1 + 2 x a

F = q Q 4 π ϵ 0 a 2   1 - 2 x a - 1 - 2 x a

F = q Q 4 π ϵ 0 a 2   - 4 x a

F = - q Q π ϵ 0 a 3   x

Comparando com:

F = - k x

Teremos:

F = - q Q π ϵ 0 a 3   ⏞ i s s o   é   k x

Então aplicamos:

f = 1 2 π ⋅ k m

f = 1 2 π ⋅ q Q π ϵ 0 a 3   m

f = 1 2 π ⋅ q Q π ϵ 0 a 3   ⋅ m

Passo 4

( b )

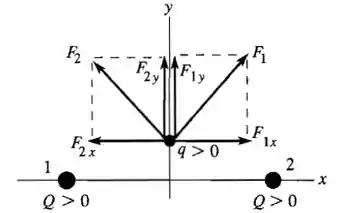
Os componentes x das forças exercidas pelas duas cargas são cancelados.

Os componentes y são adicionados e a força líquida está na direção +   y quando y >   0 e na direção - y quando y   < 0 .

A carga se afasta da origem do eixo y e não retorna.

Resposta

( a )

f = 1 2 π ⋅ q Q π ϵ 0 a 3   ⋅ m

( b )

Os componentes x das forças exercidas pelas duas cargas são cancelados.

Os componentes y são adicionados e a força líquida está na direção +   y quando y >   0 e na direção - y quando y   < 0 .

A carga se afasta da origem do eixo y e não retorna.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 22-31, as quatro partículas são mantidas fixas e têm cargas q 1 = q 2 = +Se, q 3 = +3e e q 4 = - 12e. A distância d= 5,0 μm. Qual é o módulo do campo elétrico no ponto P?
A Fig. 22-34 mostra duas partículas carregadas mantidas fixas no eixo x : - q =- 3,20 · 10 - 19C , no ponto x = -3,00m , e q = 3,20 · 10 - 19C , no ponto x = + 3,00m . Determine (a) o módulo e (b) a o
Na Fig. abaixo, a partícula 1, de carga q 1 = - 5,00q, e a partícula 2, de carga q 2 = +2,00q, são mantidas fixas no eixo x. (a) E que ponto do eixo, em termos da distância L, o campo elétrico total é
A Fig. 22-37 mostra um arranjo irregular de elétrons (e) e prótons (p) em um arco de circunferência de raio r = 2,00c m , com ângulos θ 1 = 30,0 ° , θ 2 = 50,0 ° , θ 3 = 30,0 ° e θ 4 = 20 , 0 ° . Dete
O núcleo de um átomo de plutônio 239 contém 94 prótons. Suponha que o núcleo é uma esfera com 6,64f m de raio e que a carga dos prótons está distribuída uniformemente na esfera. Determine (a) o módulo