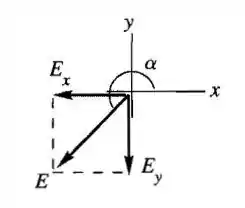
Repita o Exercício supondo que a carga situada no ponto , seja positiva e que a outra carga seja negativa, cada qual com módulo .
Passo 1
O raciocínio será análogo, ocorrerá mudanças de sinas e devemos ter atenção a atração e repulsão das cargas...
Eventualmente vamos aproximar os valores para simplificar as coisas.
O esquema será:

Vamos aplicar:
Passo 2

Passo 3
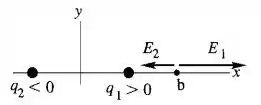
Passo 4
Como: