Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 74
21.74 Duas esferas idênticas de massa estão suspensas em fios de seda de comprimento , como indicado na . Cada esfera possui a mesma carga; logo. O raio de cada esfera é muito pequeno em comparação à distância entre as esferas, de modo que elas podem ser consideradas cargas puntiformes. Mostre que, se o ângulo for pequeno, a distância no equilibrio entre as esferas será dada por . (Sugestão: quando for pequeno, então .)
Passo 1
A questão diz que:
quando for pequeno, então
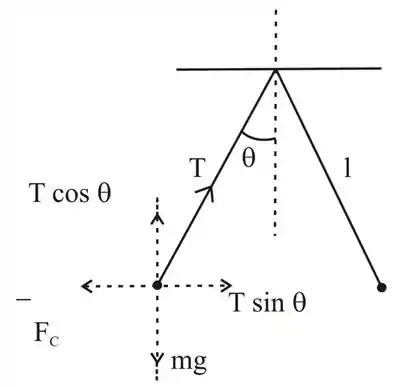
Como,
Fazemos:
Resposta
Exercícios de Livros Relacionados
Duas contas carregadas estão sobre o anel da Fig. a que possui um raio R = 60,0 cm. A conta 2, que não aparece na figura, é mantida fixa. A conta 1 está inicialmente no eixo x, na posição θ = 0 ° , ma
A Fig. abaixo mostra um próton (p) no eixo central de um disco com uma densidade uniforme de cargas devido a um excesso de elétrons. Três dos elétrons são mostrados na figura: o elétron e c no centro
A Fig. Abaixo mostra um anel de plástico de raio R = 50,0 cm. Duas pequenas contas coloridas estão sobre o anel: a conta 1, de carga +2,00 μC, que é mantida fixa na extremidade esquerda, e a conta 2,
Na Fig. abaixo, as quatro partículas formam um quadrado de Iado a = 5,00 cm e têm cargas q 1 = + 10,0 nC, q 2 = -20,0 nC, q 3 = + 20,0 nC e q 4 = -10,0 nC. Qual é o campo elétrico no centro do quadrad
Duas partículas são mantidas fixas no eixo x: a partícula 1, de carga - 2,00x10 - 7C , no ponto x = 6,00 cm, e a partícula 2, de carga 2,00x10 - 7C , no ponto x = 21,0 cm. Qual é o campo elétrico tota