Duas pequenas esferas idênticas, de massa , estão suspensas por fios de seda de comprimento e presos em um ponto comum . Cada esfera possui a mesma carga; logo, . Cada fio possui inclinação com a vertical. Faça um desenho mostrando as forças que atuam sobre cada esfera. Considere as esferas como cargas puntiformes. Calcule o módulo de . Os dois fios agora se encurtam para um comprimento , enquanto as cargas e ficam inalteradas. Qual será o novo ângulo que cada fio formará com a vertical? (Sugestão: esta parte do problema pode ser resolvida numericamente pelo método do das tentativas; escolha um valor inicial para e ajuste os valores de até obter um valor autoconsistente com a resposta.)
Passo 1
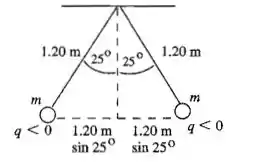
O diagrama do corpo livre fica, para esquerda e direita, respectivamente:
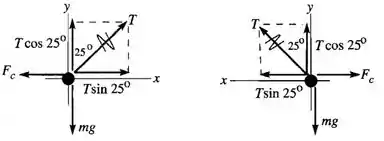
Passo 2
Como,
Fazemos:
Sabendo que:
Isolando da expressão chegamos em:
Passo 3
Já sabemos que:
Vamos pôr o como variável , e pôr os ângulos como e desenvolver:
Agora vamos considerar o e achar um valor referência do lado direito e chutar valores por tentativa e erro (método numérico) e achar :
Podemos começar a chutar valores para , mas como sabemos que pequeno, chegamos há essa já pode ser a resposta, mas vamos seguir o conselho do autor e realizar um método numérico, mas já sabemos que o ângulo é menor que então, fazendo:

Deu um pouco diferente de , já esperado, pois esse valor também foi achado por aproximação, o que temos confiança em dizer é que o ângulo vai estar entre