Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo R.1 - Ex. 25
25. Seu amigo, que tem a sua idade viaja para Alfa de Centauro, a anos-luz de distância, e retorna imediatamente. Ele alega que a viagem completa durou apenas anos. Qual foi sua rapidez? Ignore acelerações da nave e de seu amigo e suponha que ele tenha viajado com a mesma rapidez durante toda a viagem.
Passo 1
Para calcular a velocidade no sistema de referência do nosso amigo, que vamos chamar de , consideremos cada etapa da viagem separadamente. Supomos um bastão imaginário que se estende da Terra para Alfa de Centauro e que está em repouso em relação a Terra. No quadro de , o comprimento do bastão e, portanto, a distância entre a Terra e Alfa de Centauro, é encurtado de acordo com a fórmula de contração de comprimento. Ao longo de três anos, no relógio de , Alfa de Centauro viaja na velocidade de sua localização inicial em relação a ele.
Vamos esbocar a situação como está no nosso quadro de referência, na Terra. A distância entre a Terra e Alfa de Centauro é o comprimento inicial do bastão. A imagem abaixo representa essa situação:
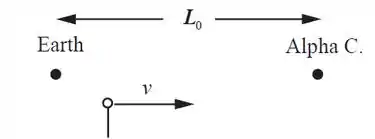
Agora vamos esboçar a situação como está no quadro de referência de . A distancia entre a Terra e Alfa de Centauro é o comprimento L contraído do bastão, conforme foi discutido. A seguinte imagem representa esse cenário:
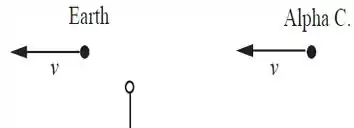
Agora, vamos deixar de figurinha e pensar no jeito de resolver nosso problema organizadamente!
Passo 2
Bom! Olhando novamente o enunciado, vamos dividir o problema em dois eventos que são, onde deixa a Terra e chega a Alfa de Centauro. No referencial de , esses dois eventos ocorrem no mesmo lugar (ao lado de ). Portanto, o tempo entre esses dois eventos é o tempo adequado entre eles. Nosso amigo do problema diz que o tempo para ir até Alfa de Centauro e retornar à Terra, foi de longos anos. Ora bolas! Como dividimos o problemas em dois eventos que são deixa a Terra e chega a Alfa de Centauro, o tempo é metade desse período, portanto igual a anos.
Agora, vamos nos concentrar no espaço! Temos que a distância percorrida por Alfa de Centauro no quadro de durante os primeiros três anos é igual à velocidade multiplicada pelo tempo no referencial de :
Passo 3
Como falado lá no , a distância entre a Terra e Alfa de Centauro no quadro de é o comprimento contraído do bastão imaginário, dado pela seguinte fórmula:
Mas :
Elevam-se os dois lados da equação ao quadrado:
Substitui-se, então, os valores numéricos correspondentes:
Resposta
A nave teve uma rapidez igual a vezes a velocidade da luz.