Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 15
| Ted está sentando em sua cadeira de jardim quando Stella passa voando diretamente acima dele a , em direção ao sudeste. Cinco segundos mais tarde, uma granada explode a leste de Ted. Quais são as coordenadas do local da explosão no referencial de Stella? Considere que, no referencial de Stella, ela própria esteja na origem, com o eixo apontando para leste.
Passo 1
Primeiro lembre-se das coordenadas:
Ted estará na origem.
Stella passará em direção (e sentido) sudeste.
A granada explode a leste de Ted.
Assim os vetores para situação vão ser:
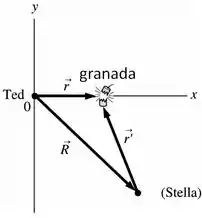
Passo 2
Por trigonometria analisando a velocidade de Stella decomposto em e :
Mas sabemos que:
A distância é o próprio ... E como a garrafa explode após a passagem por Ted, podemos reescrever a velocidade assim:
Já temos então:
Assim:
Achamos , mas essa ainda não são as coordenadas até o local da explosão, o é as coordenadas saindo da origem de Ted... Veja a imagem do
Passo 3
Mas agora que temos o , podemos relaciona-lo com e por uma soma vetorial. Assim:
Vamos achar , já sabemos que só em leste, ou seja, , assim:
)
Como a questão pede para considerar que, no referencial de Stella, ela própria esteja na origem, com o eixo apontando para leste.... As coordenadas dela até a granada é o .
)
Resposta
)