Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 8º - Capítulo 27.7 - Ex. 37

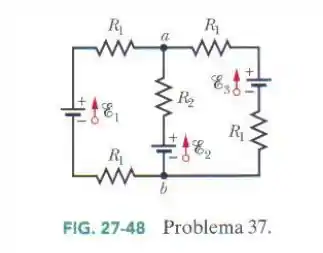
27.37. Na Fig. 27-48 as resistências R 1 = 1,0   Ω e R 2 = 2,0   Ω e as forças eletromotrizes das fontes ideias são ξ 1 = 2,0   V , ξ 2 = 4,0   V e ξ 3 = 4,0   V . Determine (a) o valor absoluto e (b) o sentido (para cima ou para baixo) da corrente na fonte 1; (c) o valor absoluto e (d) o sentido da corrente na fonte 2; (e) o valor absoluto e (f) o sentido da corrente na fonte 3; (g) a diferença de potencial V a - V b .

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui eu e você precisaremos encontrar as correntes presentes neste circuito. Gostaria de lembrá-lo que quando não temos os sentidos das correntes em um circuito, podemos arbitrariamente propor um sentido e calcularmos, caso o valor encontrado seja positivo, o sentido que propomos é o correto, caso o valor encontrado seja negativo, então o sentido que encontramos é na verdade o oposto do correto.

Passo 2

Temos o seguinte circuito

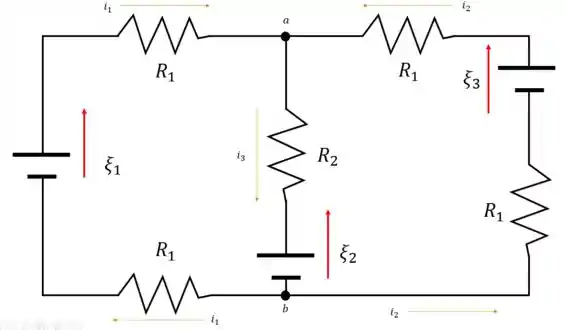
Bom, podemos ver pela imagem que em cada ramo do circuito temos dois resistores R 1 em série. Ou seja, se você for do ponto a até o b por qualquer caminho que tenha o resistor R 1 , você vai encontrar dois resistores R 1 ligados em série.

Outra coisa interessante de notar, é que pelo enunciado temos as seguintes relações

ξ 2 = ξ 3

E

R 2 = 2 R 1

Bom, vamos começar pelo item (a). Para isso vamos usar a lei das malhas, temos duas malhas na imagem, a malha da esquerda fica o seguinte

- i 1 R 1 + ξ 1 - i 1 R 1 - i 2 R 2 - ξ 2 = 0

Mas aqui é interessante notar que pela lei dos nós, a gente pode ver que

i 2 = i 1 + i 3

Então

- i 1 R 1 + ξ 1 - i 1 R 1 - i 1 + i 3 R 2 - ξ 2 = 0

- 2 i 1 R 1 + ξ 1 - i 1 + i 3 R 2 - ξ 2 = 0

Passo 3

Substituindo os valores

- 2 i 1 + 2 - i 1 + i 3 2 - 4 = 0

Então

- 4 i 1 - 2 i 3 - 2 = 0

Agora vamos fazer a malha da direita

- i 3 R 1 + ξ 3 - i 3 R 1 - i 2 R 2 - ξ 2 = 0

Logo

- i 3 R 1 + ξ 3 - i 3 R 1 - i 1 + i 3 R 2 - ξ 2 = 0

- 2 i 3 R 1 + ξ 3 - i 1 + i 3 R 2 - ξ 2 = 0

Substituindo os valores

- 2 i 3 + 4 - i 1 + i 3 2 - 4 = 0

Então

- 4 i 3 - 2 i 1 = 0

Passo 4

Agora a gente tem duas equações e duas incógnitas. A gente pode resolver esse sistema igualando as equações

- 4 i 1 - 2 i 3 - 2 = - 4 i 3 - 2 i 1

Vamos isolar i 3

4 i 3 - 2 i 3 = 4 i 1 - 2 i 1 + 2

Então

2 i 3 = 2 i 1 + 2

Então

i 3 = i 1 + 1

Agora a gente pode calcular o valor da corrente.

Vamos usar a equação da malha esquerda

- 4 i 1 - 2 i 3 - 2 = 0

- 4 i 1 - 2 i 1 + 1 - 2 = 0

Logo

- 6 i 1 - 2 - 2 = 0

Então

i 1 = - 2 3 = - 0,67   A

Mas como estamos tratando do valor absoluto

i 1 = - 0,67 A = 0,67   A

Passo 5

Agora no item (b) precisamos determinar o sentido da corrente que acabamos de calcular no item (a). O sentido da corrente é para baixo.

Vamos para o item (c). Esse calculo vai ficar muito mais fácil se usarmos as equações que deduzimos no item (a).

i 2 = i 1 + i 3

E

i 3 = i 1 + 1

Então

i 2 = i 1 + i 1 + 1

i 2 = 2 i 1 + 1

Substituindo os valores

i 2 = 2 - 2 3 + 1 = - 1 3

Então seu valor absoluto é

i 2 = - 1 3 = 1 3

Passo 6

Agora vamos determinar o sentido da corrente para responder o item (d). O sentido é para cima. Veja, o resultado deu positivo mesmo antes de aplicarmos o módulo.

Passo 7

No item (a), a gente concluiu que

i 3 = i 1 + 1

Então

i 3 = - 2 3 + 1 = 1 3

Essa é a resposta do item (e)

Agora no item (f), vamos determinar o sentido dessa corrente. Seu sentido é para cima.

Passo 8

Vamos finalmente para o último item. Para calcular a diferença de potencial podemos usar a equação

V a - V b = - i 2 R 2 + ξ 2

Isso vai dar

Δ V = - 1 3 2 + 4 = 3,3   V

Resposta

  1. 0,67   A
  2. Para baixo.
  3. 0,33   A
  4. Para baixo.
  5. 0,33   A
  6. Para cima.
  7. 3,3   V
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura 25-50, os valores das resistências estão relacionados como segue R 2 = R 3 = 2 R 1 . Se a potência P é fornecida a R 1 , qual é a potência fornecida a R 2 e a R 3 ?
Um comprimento de arame tem uma resistência de 120Ω . O arame é cortado em pedaços que têm o mesmo comprimento, e então os arames são conectados em paralelo. A resistência do arranjo paralelo é de 1,8
Uma fonte de alimentação de 5V tem uma resistência interna de 50Ω . Qual é o menor resistor que pode ser colocado em série com a fonte de alimentação para que a queda de tensão através do resistor sej
(a)Resistência a resistência equivalente entre os pontos a e b na Figura 26-56. (b) Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
A bateria na Figura 25-55 tem resistência interna desprezível. Encontre (a) a corrente em cada resistor e (b) a energia fornecida pela bateria.