Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas desafioadores - Ex. 87
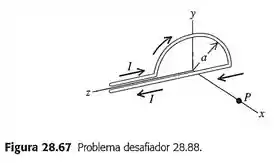
Um disco dielétrico carregado. Um disco dielétrico fino, com raio , possui uma carga total distribuída uniformemente sobre sua superfície. Ele gira vezes por segundo em torno de um eixo perpendicular à sua superfície, passando por seu centro. Calcule o campo magnético no centro do disco. (Sugestão: divida o disco em anéis concêntricos, com largura infinitesimal.)
Passo 1
O campo magnético no centro de um anel circular percorrido por corrente é:
Para carga :
Para corrente num disco girando vezes por segundo:
Voltando a
Integramos a borda do disco para :
Resposta
Exercícios de Livros Relacionados
Uma espira quadrada de lado L é percorrida por uma corrente i .Determine, em módulo, direção e sentido, o campo B → ( z ) num ponto P situado sobre o eixo da espira (reta perpendicular ao seu plano pa
No modelo de Bohr para o átomo de hidrogênio, o raio a 0 da órbita 1ª órbita circular do elétron é dado pala condição de quantização L = ℏ , onde ℏ = 1,055 × 10 - 34 J . s e L é a magnitude do momento
No modelo de Bohr para o átomo de hidrogênio, o raio a 0 da órbita 1ª órbita circular do elétron é dado pala condição de quantização L = ℏ , onde ℏ = 1,055 × 10 - 34 J . s e L é a magnitude do momento
Dois fios retilíneos paralelos muito longos (tratados como infinitos), separados por uma longa distância 2 b , transportam correntes de mesma intensidade i , em sentidos opostos (um é o retorno do out
Dois fios retilíneos paralelos muito longos (tratados como infinitos), separados por uma longa distância 2 b , transportam correntes de mesma intensidade i , em sentidos opostos (um é o retorno do out