Dois fios retilíneos paralelos muito longos (tratados como infinitos), separados por uma longa distância , transportam correntes de mesma intensidade , em sentidos opostos (um é o retorno do outro). Considere um ponto P qualquer no plano dos dois fios. Sobre a perpendicular aos fios que passa por P, tome a origem O a meio caminho entre os fios, e seja a abscissa de P em relação a O.
- Calcule a magnitude do campo magnético em P, para (supõe-se que a distância de P a cada fio é muito maior que o diâmetro do mesmo).
Passo 1
Se liga como vamos resolver o item (a)! Para entender melhor o que está acontecendo, podemos observar o desenho a seguir que representa o esquema descrito no enunciado.
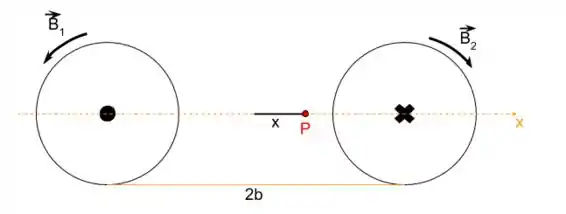
Para calcular o campo magnético, precisamos lembrar “lei de Gauss” para o magnetismo. Beleza?!
Podemos ver que a trajetória do campo é uma circunferência, então escreveremos que
Portanto
Passo 2
Para consideraremos
Para o sinal da integral será negativo, pois o campo está no sentido horário assim teremos
Como o campo no ponto é a soma dos dois campos
Fazendo o mmc, teremos: