29- O campo magnético no interior de um solenoide retilíneo longo, com seção reta circular de raio , está crescendo com uma taxa .

Qual é a taxa de variação do fluxo magnético através de um círculo de raio no interior do solenoide, perpendicular ao eixo do solenoide e centralizada sobre seu eixo?

Calcule o módulo do campo elétrico induzido no interior do solenoide, a uma distância de seu eixo. Mostre a direção e o sentido desse campo em um diagrama.

Qual é o módulo do campo elétrico fora do solenoide, a uma distância de seu eixo?

Faça um gráfico do campo elétrico induzido em função da distância de seu eixo, desde até

Qual é o módulo da fem induzida em uma espira circular de raio igual a que possui centro sobre o eixo da solenoide?

Qual será o módulo da fem induzida, se o raio da espira do item for igual a ?

E se o raio da espira do item for igual a ?

Já o cálculo para o módulo do campo elétrico será pela lei de Faraday:

Onde será o comprimento do círculo que dista do eixo do cilindro onde passa a solenoide e onde , então teremos que , então:

Então o módulo do campo elétrico será:

Tirando o módulo

Já o campo elétrico a uma distância :

Pois o fluxo magnético para fora do corpo é o fluxo magnético produzido pelo raio do solenoide, ou seja

O gráfico do campo elétrico (para a letra ) tende a crescer numa reta onde vai de até e depois que chega a o mesmo decai num valor de , com sendo uma constante e indo de até infinito nos dando um gráfico parecido com:

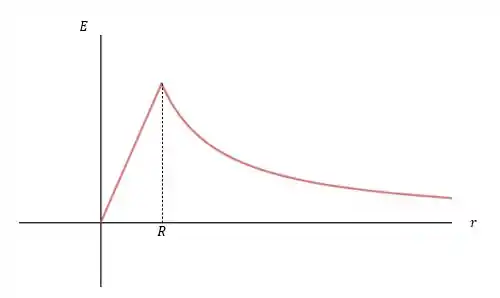
Considere como uma constante.

Na letra , como estamos dentro da solenoide , então a fem será de:

Tirando o módulo:

E para a letra caso o raio seja igual a teremos:

E caso seja :

Pois a fem depende exclusivamente da área da espira que selecionamos, não tem o comprimento dela como no campo elétrico