Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 31

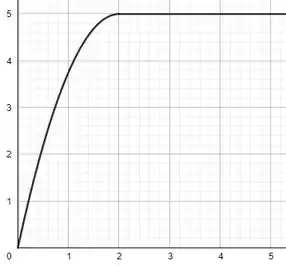
31. A FIGURA EX4.31 mostra o gráfico da aceleração versus tempo de uma plataforma giratória que parte do repouso. Desenhe um gráfico da velocidade angular versus tempo. Inclua escalas numéricas apropriadas para os eixos.

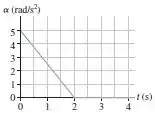
Passo 1

Então galera, para fazer o gráfico da velocidade angular podemos usar o seguinte:

α = d ω d t

⇒ d ω = α d t

Assim temos que:

ω = ∫ α   d t

Assim encontramos uma função ω ( t ) e podemos montar o gráfico.

Mas para isso precisamos uma função α ( t ) , temos que de t = 0 até t = 2   s temos um comportamento linear de alpha, logo podemos encontrar a função que define essa parte do gráfico assim:

α - α 0 = - Δ α Δ t ( t - t 0 )

E de t = 2   s em diante temos que α = 0 , logo integrando isso temos que ω é constante.

Passo 2

Vamos então encontrar a função para α de t = 0 até t = 2   s , temos:

α - 5 = - 5 2 ( t - 0 )

⇒ α = - 2,5 t + 5

Agora podemos encontrar uma função para ω , temos:

ω = ∫ α   d t

⇒ ω t = ∫ - 2,5 t + 5 d t

Temos então que:

ω t = - 2,5 t 2 2 + 5 t

⇒ ω t = - 1,25 t 2 + 5 t

Agora temos o que precisamos para fazer o gráfico da velocidade angular.

Passo 3

Temos então seguinte gráfico:

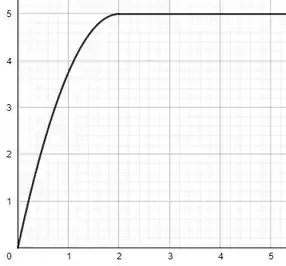
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro viajando em uma pista circular plana (sem inclinação) acelera uniformemente do repouso com aceleração tangencial de 1,70m / s 2 . Ele chega a um quarto do trajeto ao redor do círculo antes qu
Um carro viajando em uma pista circular e plana (sem inclinação) acelera uniformemente do repouso com uma aceleração tangencial de a . Ele chega a um quarto do caminho ao redor do círculo antes que de
Uma barra em uma dobradiça começa do repouso e gira com aceleração angular α =( 10+6t ) , onde está em r a d / s 2 e t em segundos. Determine o ângulo em radianos pelo qual a barra gira nos primeiros
Uma centrífuga em um laboratório médico gira com velocidade angular de 3.600r e v / m i n . Quando é desligada, ela gira por 50,0r e v o l u ç õ e s çõ antes de parar completamente. Encontre a acelera
Um Compact Disc de áudio digital carrega dados; cada bit ocupa 0,6μ m ao longo de uma faixa espiral contínua a partir da circunferência interna do disco para a extremidade externa. Um CD player gira o