Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 32
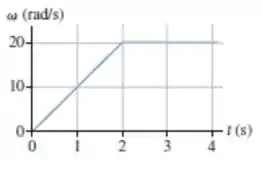
32. A FIGURA EX4.32 mostra o gráfico da velocidade angular versus tempo para uma partícula que se move em um círculo. Quantas revoluções o objeto realiza nos primeiros ?
Passo 1
Então galera para sabermos quantas revoluções a partícula realizou precisamos saber o deslocamento angular dela.
Mas por quê? Pois temos que em uma revolução temos um deslocamento angular de , assim basta dividir o deslocamento que encontrarmos por e encontramos o número de revoluções.
Para encontrar o deslocamento angular nesses mostrados no gráfico, podemos usar o fato de que o deslocamento angular é iguala a área do gráfico da velocidade angular.
De até temos que o nosso gráfico é um trapézio e a área do trapézio é dada por:
Onde é a base maior do trapézio, é a base menor e é altura do trapézio.
Assim para nossa situação temos que:
Passo 2
Vamos então encontrar o deslocamento angular e depois encontrar o número de revoluções, temos:
Sabendo disso agora só temos que dividir esse valor por e encontramos o número de revoluções, assim: