Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 36
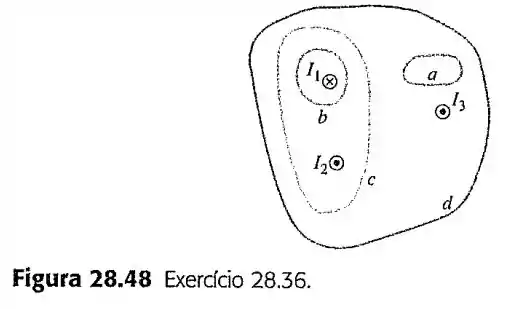
36- A figura mostra a seção reta de diversos condutores que conduzem correntes que atravessam o plano da figura. Os sentidos das correntes são indicados na figura e os módulos são e . Quatro trajetórias indicadas pelas letras de até são mostradas na figura. Qual é o valor da integral de para cada trajetória? Para cada integral, escolha um percurso no sentido anti-horário. Explique suas respostas.
Passo 1
O valor da integral de linha do campo magnético em uma região fechada é igual a:
Onde o sentido anti-horário é o sentido positivo. Em outras palavras imagina uma região qualquer e nela passa uma corrente que sai da folha do papel, essa corrente pela regra da mão direita produzirá um valor positivo desse somatório de campo-metro igual a:
Pois gera um campo magnético positivo para essa integral.
Passo 2
Então podemos começar, não existe nenhuma corrente que passa por esse caminho então essa região não contribui em nada com a integral de linha, então:
Passo 3
A região por outro lado possui uma corrente que entra na folha do papel igual a , então ela contribui no sentido horário para a integral de linha, portanto dando um resultado negativo, ou seja:
Passo 4
Já na região temos a presença de duas correntes, a corrente que já falamos no caso anterior e a corrente que contribui positivamente (pela regra da mão direita) para a integral
de linha então:
Passo 5
E finalmente a região que tem todas as correntes. Aqui já deve ter ficado claro que as correntes que saem do plano contribuem positivamente para a integral de linha (pois geram campos magnéticos no sentido anti-horário) enquanto as horárias são negativas: