Uma linha de transmissão de corrente contínua conduz correntes opostas em seus cabos paralelos separados por . Sendo a corrente em cada cabo, calcule a força de repulsão por metro linear dos cabos.

Fala galerinha, bora resolver um problema sobre força entre fios?

Você deve ter lido na seção 22.3 do livro sobre a interação entre duas correntes né? Você deve ter visto que quando as correntes estão no mesmo sentido os fios se atraem, enquanto quanto as correntes têm sentidos opostos eles se repelem.

A ideia básica sobre de onde vem essa força é a seguinte: um dos fios vai gerar um campo magnético na região em que o outro fio está. O campo gerado por um fio com corrente a uma distância é dado por

A direção e sentido desse campo é dada pela regra da mão direita:

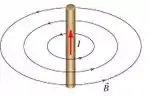
Daí, suponha que o outro fio está a uma distância do primeiro. O campo magnético será perpendicular a corrente, de modo que aparece uma força dada pela fórmula do “Bil”:

Essa expressão foi deduzida no capítulo 21 do livro, vai lá dar uma olhadinha especial na seção 21.8.

Vou chamar a corrente do fio que gera o campo de e a corrente no fio em que atua a força de :

Substituindo uma equação na outra, você vai encontrar

Ou ainda,

Essa é a expressão da força por unidade de comprimento que também foi deduzida na seção 22.3 do livro.