Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 21
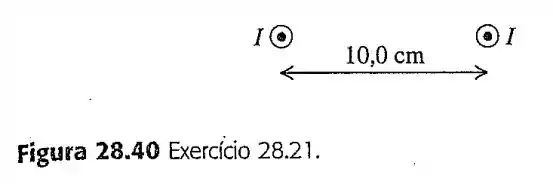
21- Dois fios longos, retilíneos e paralelos estão separados por uma distância de e transportam correntes iguais de no mesmo sentido, como indica a Figura . Determine o módulo, a direção e o sentido do campo magnético.
no ponto que é o ponto médio entre os fios;
no ponto , a esquerda de
no ponto , diretamente acima de .
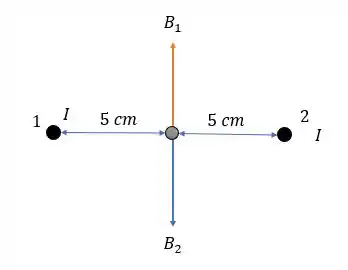
Passo 1
Vamos escrever o sentido entrando no papel como e saindo do papel com , e a distância horizontal como , dessa forma para a letra cada corrente nos dará um campo magnético igual a:
Pois para vetores de uma dimensão podemos escrever:
Podíamos analisar também pela regra da mão direita, pois como temos corrente no mesmo sentido então o campo magnético do fio a esquerda será positivo em enquanto outro será negativo. Porém pela forma vetorial fica mais fácil de ver isso.
Nos deixando com a seguinte representação:
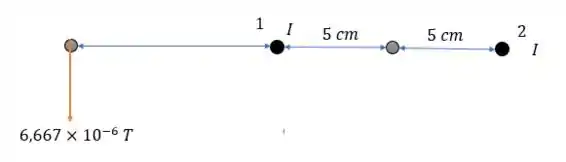
Passo 2
O ponto a esquerda de será um ponto a esquerda do fio a esquerda então teremos o seguinte campo total em .
Como .
Com atribuindo a maior influência nesse campo.
Passo 3
Agora acima de nós teremos:
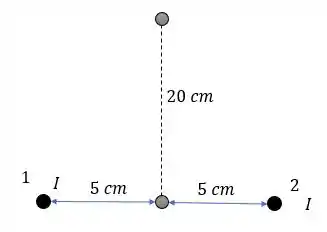
Então o campo magnético em será:
Quando temos dois valores de coordenada para temos que fazer então:
Substituindo e será:
Apontando para a direita