Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 52
Uma bola de gira descrevendo um círculo vertical presa na ponta de um fio com 80 cm de comprimento. A tensão no fio é de quando ele forma um ângulo com a vertical.
a. Qual é a rapidez da bola quando
b. Qual é o módulo e qual é a orientação da aceleração da bola quando?
Passo 1
Olá, tudo bem?
Antes de qualquer coisa, vamos fazer um desenho da situação:
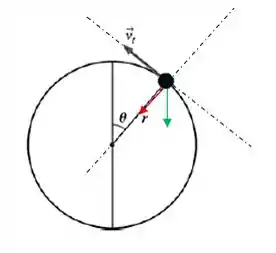
Em verde está representada a força peso e em vermelho a força tensora . O ângulo que a força peso faz com a linha tracejada na direção radial é . Na direção radial temos uma força resultante que aponta para o centro da trajetória, e na direção tangencial temos que a resultante é igual ao produto da massa pela aceleração tangencial . Então podemos formar o seguinte sistema de equações:
Os dados que o problema nos dá são os seguintes:
Passo 2
Letra a)
O problema nos pede a velocidade tangencial , então usando a primeira equação do nosso sistema e os dados que o enunciado deu, temos:
Tranquilo? Vamos pra letra (b) então!
Passo 3
Letra b)
Agora o problema pede o módulo e a orientação da aceleração. Precisamos lembrar como calculamos isso:
Precisamos encontrar a aceleração radial, a aceleração tangencial e aplicar nessas formulinhas ali em cima.
Começando pela aceleração tangencial Da segunda equação do nosso sistema temos:
Agora a aceleração radial:
Agora é só aplicar nas relações anteriores para o módulo e a orientação:
Beleza?
Espero ter ajudado!
Vamos pra próxima?