Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 68

Na Fig. 8-36, a corda tem um comprimento L = 120   c m e possui uma bola presa em uma das extremidades, enquanto a outra está fixa. Existe um pino no ponto P . Liberada a partir do repouso, a bola desce até a corda tocar o pino; em seguida, a bola sobe e começa a girar em torno do pino. Qual é o menor valor da distância d para que a bola dê uma volta completa em torno do pino? (Sugestão: a bola deve ainda estar se movendo no ponto mais alto da volta. Você sabe por quê?)

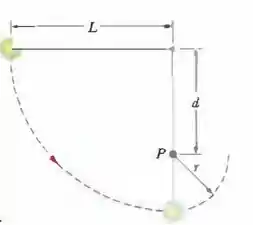
Figura 8-36 Problema 70

Passo 1

No ponto mais alto depois que a corda encosta no pino, temos a tração e força peso apontando para baixo, na direção do raio

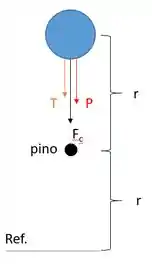
A resultante das forças na direção do raio é chamada força centrípeta e é dada por

F r = F c = m v 2 r

Como só temos duas forças agindo no corpo e adotando o sentido para baixo como positivo.

T + P = m v 2 r

A bola passando com a menor velocidade possível na situação da figura acima, temos a tração da corda nula, logo

P = m v 2 r

m g = m v 2 r

v 2 = g r

Para L = r + d   → r = L - d

v 2 = g ( L - d )

Passo 2

Aplicando o princípio da conservação mecânica no início do movimento ( 1 ) e quando a bola atinge o ponto mais alto depois que a corda encosta no pino ( 2 ), temos

K 1 + U 1 = K 2 + U 2

Tomando como referência da energia potencial o ponto mais baixo do movimento. No ponto 1 a energia cinética é nula (objeto parte do repouso) e a energia potencial gravitacional é dada por

U 1 = m g h = m g L

No ponto 2

U 2 = m g h = m g 2 r = 2 m g L - d

E

K 2 = 1 2 m v 2 = 1 2 m g ( L - d )

Passo 3

Logo, substituindo na lei da conservação mecânica

m g L = 2 m g L - d + 1 2 m g L - d

L = L - d 2 + 1 2

L = L - d 5 2

L - d = 2 L 5

d = L - 2 L 5

d = 3 L 5

Para L = 1,2   m

d = 3.1,2 5

d = 0,72   m

Resposta

A menor distância d para que a bola dê uma volta completa em torno do pino é d = 0,72   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Bombardeio com próton. Um próton com massa igual a 1,67× 10 - 26k g é impulsionado com uma velocidade inicial de 3,0 x 105 m/s diretamente contra um núcleo de urânio situado a uma distância de 5,0 m.
Um bloco de 5,0 kg se move com v0 = 6,0 m/s sobre uma superfície horizontal sem atrito, dirigindo-se contra uma mola cuja constante é dada por k = 500 N/m e que possui uma de suas extremidades presa a
Uma balança de mola é calibrada de tal forma que o prato desce 1cm quando uma massa de 0,5 Kg está em equilíbrio sobre ele. Uma bola de 0,5 Kg de massa fresca de pão guardada numa prateleira 1m acima
No sistema da figura, M= 3 Kg, m= 1 Kg e d = 2 m. O suporte S é retirado num dado instante. a) Usando conservação de energia, ache com que velocidade M chega ao chão. b) Verifique o resultado, calcula
Resolva o problema 8 do capítulo 4 a partir da conservação de energia.