55 - Ressonância em paralelo. A impedância em um circuito R-L-C em paralelo foi deduzida no Problema 31.54.
- Mostre que na ressonância a frequência angular é dada por , e é um mínimo.
- Como é um mínimo na ressonância, é correto dizer que a potência fornecida ao resistor é um mínimo para ? Explique.
- Na ressonância, qual é o ângulo de fase da corrente que passa na fonte em relação à voltagem da fonte? Como isso se compara com o ângulo de fase em um circuito R-L-C em série durante a ressonância?
- Faça um diagrama do circuito para um circuito R-L-C em paralelo. Em seu diagrama, coloque o resistor mais próximo da fonte e os outros elementos mais afastados. Justifique a seguinte afirmação: Quando a frequência angular da fonte é não existe nenhuma corrente circulando entre () a parte do circuito incluindo a fonte e o resistor e (ii) os dois elementos do circuito incluindo o indutor e o capacitor, de modo que seria possível cortar os fios que ligam essas duas partes do circuito sem alterar o valor das correntes.
- A afirmação mencionada no item (d) ainda permanece válida quando consideramos que qualquer indutor e capacitor real possui uma pequena resistência? Explique.
Passo 1
Bem, o sistema paralelo é esse daqui:
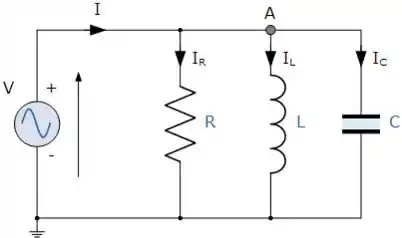
Poxa, vimos no exercício passado () que a corrente de um circuito paralelo pode ser encontrada assim:
Para encontrarmos a frequência de ressonância, devemos cancelar a parte que veio das reatâncias capacitivas e indutivas. Em outras palavras...
Bem semelhante ao que tínhamos no caso série . e são calculados usando a Lei de Ohm e as reatâncias...
Só que na ressonância, (as reatâncias são iguais):
E por último... SIM! é o menor possível na ressonância, já que ...
Passo 2
Na verdade não é o correto dizer isso, a final a potência fornecida ao resistor não muda é sempre:
O que muda é a corrente , mas a corrente continua intacta e ela só muda se (tensão da fonte) mudar, saca?
Passo 3
Ora, na ressonância, vimos que...
Como não tem nenhum nem nada, essa equação indica que a corrente vai estar em fase com a tensão (tem o mesmo ângulo), afinal é um valor escalar e ele só vai mudar o módulo, mas não o ângulo.
Isso tudo indica que o circuito em paralelo é bem análogo ao em série, afinal lá a gente também tínhamos uma corrente em fase com a tensão!
Passo 4
O diagrama pedido do circuito é esse daqui que gente já viu no inicio do exercício para simplificar o problema:
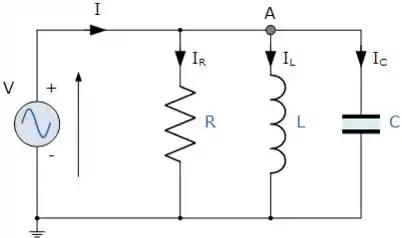
Vamos avaliar agora as duas afirmações, começando pela primeira:
“Quando a frequência angular da fonte é não existe nenhuma corrente circulando entre () a parte do circuito incluindo a fonte e o resistor”.
Essa afirmação é falsa, já que a corrente vai sair da fonte e indo para o resistor, saca? Agora a segunda afirmação:
“Quando a frequência angular da fonte é não existe nenhuma corrente circulando entre (ii) os dois elementos do circuito incluindo o indutor e o capacitor, de modo que seria possível cortar os fios que ligam essas duas partes do circuito sem alterar o valor das correntes.”
De fato essa afirmação número é verdadeira, afinal na ressonância vimos que em módulo:
E toda corrente do circuito é a corrente que passa pelo resistor, de modo que podemos cortar o circuito em sem alterar as correntes:
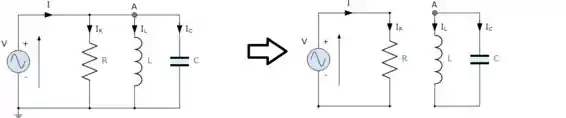
Passo 5
Poxa, se o indutor ou o resistor possuírem uma pequena resistência, vai existir sempre uma corrente que vai passar da fonte para o elemento onde tem a pequena resistência, o que significa que não vai ser mais igual a mais no problema. Logo, a sentença se torna falsa, saca?
Resposta
Ei, a resposta está no passo a passo :)