58- Um projetista de eletroímã neófito afirma ser capaz de projetar um eletroímã que produza um campo magnético no vácuo, que aponte sempre no sentido do eixo em todos os pontos da região e cujo módulo cresça com o aumento da distância . Ou seja, , em que e são constantes com unidades de teslas e de metros, respectivamente. Aplique a lei de Gauss para o campo magnético para provar que esse projeto é impossível. (Sugestão: use uma superfície gaussiana em forma de caixa retangular com arestas paralelas aos eixos e )

A superfície que a questão pede para a gente testar esse campo magnético milagroso aí é:

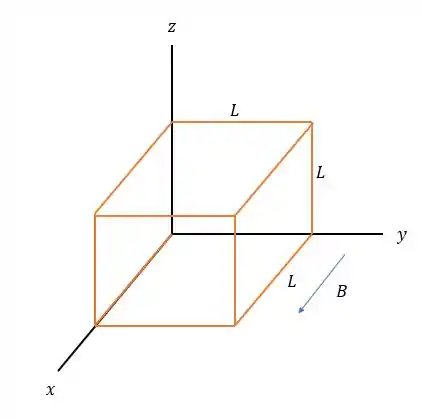
E como só temos campo magnético em então as únicas faces que tem fluxo magnético são as áreas nos planos , tanto a que está na frente quanto atrás, então pela Lei de Gauss do magnetismo temos:

Onde , logo para e para , então aplicando a Lei de Gauss, sabendo que a área desses elementos é de teremos:

E essa fórmula só estará certa se , qualquer outro valor de estará errado pois quebraria a Lei de Gauss para o magnetismo.