Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 77
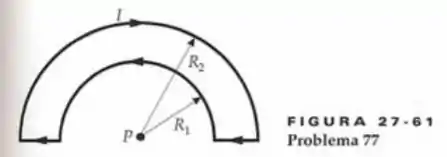
Passo 1
Seja fora da página a direção +x. Como o ponto P é na linha que conecta os segmentos retos do condutor, esses segmentos não contribuem para o campo magnético em P. Portanto, o campo magnético resultante em P será a soma dos campos magnéticos devido à corrente nos dois semicírculos, e podemos usar a expressão para o campo magnético no centro de um anel de corrente para encontrar .
Expresse o campo magnético resultante em P:
Expresse o campo magnético no centro de um anel de corrente:
onde R é o raio do anel.
Passo 2
Expresse o campo magnético no centro de meio anel de corrente:
Expresse e :
Substitua na primeira equação para obter:
Resposta
Exercícios de Livros Relacionados
A figura 29-36a mostra um elemento de comprimento d s = 1,00μ m em um fio retilíneo muito longo percorrido por corrente. A corrente no elemento cria um campo magnético elementar d B → no espaço em vol
Na figura 29-42, uma corrente i = 10A circula em um condutor longo formado por dois trechos retilíneos e uma semicircunferência de raio R = 5,0m m e centro no ponto a . O ponto b fica a meio caminho e
Na figura 29-41, dois fios retilíneos longos, separados por uma distância d = 16,0c m , conduem correntes i 1 = 3,61m A e i 2 = 3,00 i 1 dirigidas para fora do papel. (a) Em que ponto do eixo x o camp
A figura 29-52 mostra dois fios. O fio de baixo conduz uma corrente i 1 = 0,40A e inclui um arco de circunferência com 5,0c m de raio e centro no ponto P , que subtende um ângulo de 180 ° . O fio de c
Dois fios longos são paralelos e estão separados por uma distância de 8,0c m . As correntes nos fios são iguais e o campo magnético em um ponto situado exatamente a meio caminho entre os dois fios tem