Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas Desafiadores - Ex. 76
Um capacitor esférico isolado possui carga sobre o condutor interno (raio ). A seguir, metade do volume entre os dois condutores é preenchida por um dielétrico líquido com uma constante conforme indicado na seção reta da Figura 24.42. (a)Determine a capacitância do capacitor preenchido até a metade. (b)Calcule o módulo de no volume entre os dois condutores em função da distância ao centro do capacitor. Forneça respostas para a metade superior e para a metade inferior desse volume. (c) Determine a densidade de cargas livres superficial sobre o condutor interno e sobre o condutor externo. (d)Calcule a densidade de cargas ligadas superficial sobre a superíficie interna do dielétrico () e sobre a superfície externa do dielétrico (. (e)Qual é a densidade de carga ligada sobre a superfície plana do dielétrico? Explique.
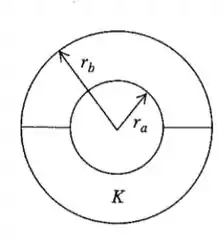
Passo 1
Temos que:
Aplicaremos a lei de Gauss e a relação entre a diferença potencial e o campo elétrico. Cada condutor tem uma superfície equipotencial.
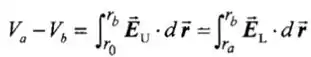
Logo,
Onde esses são os campos entre os hemisférios de cima e de baixo. O campo elétrico é o mesmo no espaço de ar como no dielétrico.
Passo 2
(a)Para um capacitor esférico normal com o ar entre as placas,
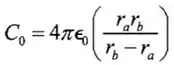
O capacitor nesse problema é equivalente a dois capacitores pararelos, e , no qual com metade da área da placa de um capacitor normal.
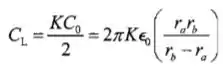
E,
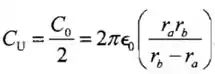
Logo,
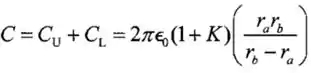
Passo 3
(b) Usando uma superfície Gaussiana hemisférica para cada respectiva metade,
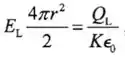
Logo,
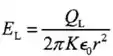
E,
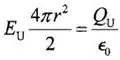
Portanto,
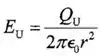
Mas,
E,
Também,
Portanto,
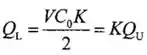
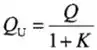
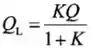
Isso nos dá que:
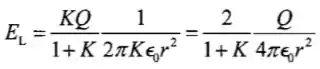
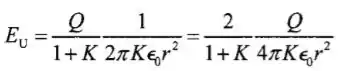
Logo, encontramos que:
Passo 4
(c)A densidade de carga livre nos hemisférios de cima e de baixo são:
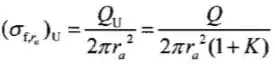
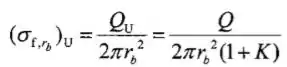
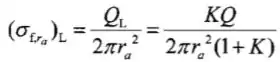
E,
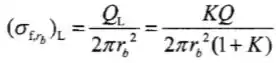
(d)
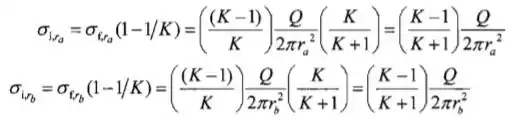
(e)Tem um carga com limite zero na superfície plana da superficie dielétrico com o ar. Isso implicaria um campo elétrico circuferencial, ou que isso seria um campo elétrico mudado assim que a carga circundaria a esfera.
Resposta
Ei, a resposta está no passo a passo :)