Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 36.Problemas - Ex. 63
63. No final da Seção , fizemos algumas afirmações sobre uma rede com fendas. Desenhe um diagrama de fasores para explicar cada uma dessas afirmações: Ocorre um mínimo quando é um múltiplo inteiro de , exceto quando for um múltiplo inteiro de (que fornece um máximo principal), Existem mínimos entre dois máximos principais consecutivos.
Passo 1
Então temos que provar as afirmativas com diagramas de fasores.
Mas vamos enterder antes cada afirmativa. Primeiro a afirmativa .
Para que tenhamos máximos para fendas temos que a soma de todas as diferenças de fase provocadas por cada fenda seja zero (na linguagem do diagrama de fasores quer dizer que eles se fecham).
Então temos que a cada diferença de fase para não sendo um múltiplo inteiro de teremos um mínimo e quando for um múltiplo de teremos o máximo independente de .
Vamos entender o item .
Como falamos em se a soma de todas as diferenças de fase nos dá um máximo e antes disso temos mínimos então temos mínimos, pois a parti do momento que adicionar mais uma fase teremos fases nos dando um máximo.
Agora vamos ver o diagrama de fasores e identificar essas afirmações.
Passo 2
Para desenhar esse diagrama de fasores temos que considerar uma situação hipotética. Vamos considerar o caso com fendas, assim e . Então nosso diagrama fica da seguinte forma:
Se você reparar ele se fecha então temos um máximo, mas isso só acontece quando temos fasores onde cada fasor representa uma diferença de fase pois assim ficamos com tendo um máximo.
Agora enquanto os fasores não se fecham temos mínimos já que teremos que é um múltiplo inteiro de com .
Passo 3
Agora vamos pegar a mesma situação hipotética para explicar , então temos:
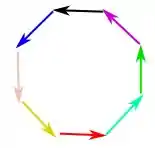
Como vimos no item temos o máximo quando temos diferenças de fase pois teremos um múltiplo de , mas enquanto isso não ocorre teremos múltiplos inteiros de (mínimos) logo até teremos mínimos então teremos mínimos.
Resposta
Ei, a resposta está no passo a passo :)