Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 25.Problemas - Ex. 64

64- A região entre duas esferas concêntricas condutoras com raios a e b está preenchida por um material condutor com resistividade ρ .

( a ) Mostre que a resistência entre as esferas é dada por

R = ρ 4 π 1 a - 1 b

( b ) Deduza uma expressão para a densidade de corrente em função do raio em termos da diferença de potencial V a b entre as esferas.

( c ) Mostre que o resultado da parte ( a ) se reduz ao resultado da Equação ( 25.10 ) quando a distância entre as esferas L = b - a é pequena.

Passo 1

A região dita no enunciado é essa aqui:

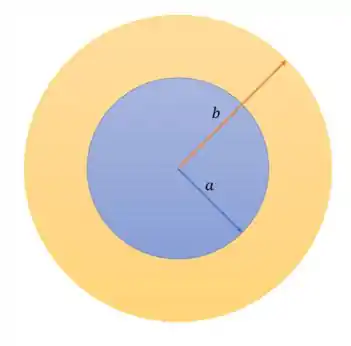
Onde a área ocupada pelo material é a região amarela e se dividirmos a região em esferas iguais de espessura d r , então:

R = ∫ ρ d r A

Onde a área de uma casca de esfera vale A = 4 π r 2 então como a espessura vale d r logo.

R = ρ ∫ a b d r 4 π r 2

Então:

R = ρ 4 π ∫ a b d r r 2

R = ρ 4 π - 1 r a b

R = ρ 4 π 1 a - 1 b

Como queríamos mostrar.

Passo 2

A corrente que passa nessa região será de:

V a b = I R

I = V a b ρ 4 π 1 a - 1 b = V a b ρ b - a 4 π a b = V a b 4 π a b ρ ( b - a )

Então a densidade de corrente será:

J = I A = V a b 4 π a b ρ b - a 4 π r 2 = V a b a b ρ b - a r 2

Considerando um raio r qualquer.

Passo 3

Rearrumando o que encontramos :

R = ρ 4 π 1 a - 1 b

Temos:

R = ρ 4 π b - a a b

Onde L = b - a e a ≈ b então:

R = ρ L 4 π a 2

Como a área da esfera é de 4 π r 2 então a equação R = ρ L A se faz válida novamente. Pois b vai ser muito parecido com a diminuindo a área amarela.

Resposta

b )   J = V a b a b ρ b - a r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de cobre de calibre 10 conduz uma corrente de 20A . Considerando que o cobre tenha um elétron livre por átomo, calcule a rapidez de deriva dos elétrons livres no fio.
O vento solar consiste em prótons vindo do sol em direção à Terra (o vento é constituído, na verdade, por 95% de prótons.) A densidade do número de prótons a uma distância do Sol igual ao raio da órbi
Um fio de ouro tem seção transversal com diâmetro de 0,10m m . As extremidades deste fio estão conectadas aos terminais de uma bateria de 1,5V . Se o comprimento do fio é 7,5c m , quanto tempo, em méd
Em um dos feixes que colidem em um supercolisor de prótons, os prótons estão se movendo com velocidades aproximadamente iguais à velocidade da luz e a corrente do feixe é 5,00m A . A densidade de corr
Um acelerador produz um feixe de prótons com uma seção circular de 2,0m m de diâmetro e corrente de 1,0m A . A densidade de corrente está uniformemente distribuída no feixe. A energia cinética de cada