Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 25.Problemas - Ex. 63

63- Um material com resistividade ρ possui a forma de um cone truncado com altura h e raios r 1 e r 2 nas suas extremidades (Figura 25.40).

( a ) Calcule a resistência do cone entre as duas faces planas (Sugestão: Divida o cone em muitos discos finos e calcule a resistência de um desses discos.)

( b ) Mostre que seu resultado está de acordo com Equação ( 25.10 ) quando r 1 = r 2

Passo 1

A resistência normalmente é dada por:

R = ρ l A

Considerando um fio de área de seção transversal constante e igual a A , porém nesse caso a seção transversal é variável com a altura e será de:

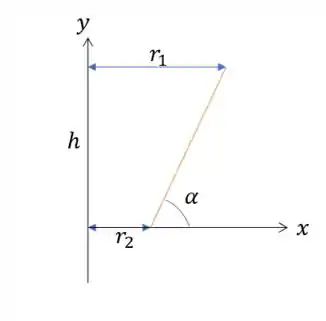
Onde temos um raio que segue a equação de reta igual a:

r = r 2 + r 1 - r 2 h y

Dúvida só fazer

x = x 0 + t g   α   y

Com x 0 sendo a distância quando x = 0 e t g   α nos diz a inclinação.

Então a resistência desse objeto será a integral:

R = ∫ 0 h ρ d y π r 2 + r 1 - r 2 h y 2

Passo 2

Integral chata mas vamos devagar:

R = ρ π ∫ 0 h d y r 2 + r 1 - r 2 h y 2

Fazendo a substituição:

u = r 2 + r 1 - r 2 h y

Nós teremos:

d u = r 1 - r 2 h d y

Logo:

d u × h r 1 - r 2 = d y

Então a integral indefinida fica como:

R = h r 1 - r 2 ρ π ∫ 1 u 2 d u

R = h r 1 - r 2 ρ π - 1 u

Voltando ao domínio de y temos:

R = h r 1 - r 2 ρ π - 1 r 2 + r 1 - r 2 h y 0 h

O que nos dá:

R = h ρ π ( r 1 - r 2 ) - 1 r 1 + 1 r 2

R = h ρ π ( r 1 - r 2 ) r 1 - r 2 r 1 r 2

R = h ρ r 1 r 2 π

Passo 3

Quando r 1 = r 2 temos:

R = ρ h π r 1 2

O que bate com a equação

R = ρ l A

Pois A = π r 1 2 que é a área de círculo constante de raio igual a r 1 e o comprimento dessa rolha é l = h , então tudo nos conformes.

Resposta

a )   R = h ρ r 1 r 2 π

b ) R = ρ h π r 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

30- Um cilindro oco de alumínio tem 2.50m de comprimento, raio interno de 3.20c m e raio externo de 4.60c m . Trate cada superfície (interna, externa e as duas faces nas extremidades) como uma superfí
23- Um corpo sólido retangular de puro germânio mede 12c m × 12c m × 25c m . Supondo que cada uma das suas faces é uma superfície equipotencial, qual é a resistência entre as faces opostas que estão (
27- ( a ) Qual é a resistência de um fio de nicromo para 0.0 ° C , se sua resistência é igual a 100.0 Ω para 11.5° C ? ( b ) Qual é a resistência de uma barra de carbono a 25.8° C , se sua resistência
25- Um fio de ouro com diâmetro igual a 0.84m m conduz uma corrente elétrica. O campo elétrico no fio é igual a 0.49V / m . Qual é ( a ) a corrente elétrica no fio ( b ) a diferença de potencial entre
57- Um condutor elétrico projetado para transportar correntes elevadas possui comprimento de 14.0m e uma seção reta circular com diâmetro de 2.50m m . A resistência entre suas extremidades é igual a 0