Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 67

67. Nos problemas de 64 a 67 , são fornecidas equações para serem usadas na resolução de um problema. Para cada uma delas, você deve

  1. Redigir um problema realista para o qual esta equação se aplique.
  2. Desenhar uma representação pictórica do tipo antes-e-após.
  3. Obter a solução do problema proposto.

Passo 1

Analisando a equação podemos ver que ela se trata de uma equação da conservação de energia mecânica. Essa equação pode ser mostrada da seguinte forma:

  1 2 m v f 2 + m g y f + 1 2 k ∆ x f 2 = 1 2 m v i 2 + m g y i + 1 2 k ∆ x i 2

Olhando os valores presentes no enunciado com sua respectiva unidade podemos dizer que se trata de um problema que possui energia cinética, potencial gravitacional e potencial elástica.

O que nos resta agora é deixar claro o que cada valor representa e resolver os itens do exercício. Então, vamos lá!

Passo 2

a ) Como vimos no Passo 1:

1 2 m v f 2 + m g y f + 1 2 k ∆ x f 2 = 1 2 m v i 2 + m g y i + 1 2 k ∆ x i 2

De acordo com o enunciado sabemos que:

1 2 0,50   k g v f 2 =   ( 0,50   k g ) ( 9,80   m / s ² ) ( - 0,10   m s e n   30 ° ) + 1 2 ( 400   N / m ) ( - 0,10   m ) ²

Podemos tirar as informações que:

m = 0,15 ,       v i = 0   m / s ,       ∆ x f = 0   m ,       ∆ x i = - 0,10   m ,       k = 400   N / m ,       y f = 0   m ,     y i = - 0,10   m s e n   30 °    

E como falta uma informação ela pode ser a estrela do nosso problema.

Passo 3

Vamos escrever o problema com a tudo o que achamos no passo anterior.

Uma mola com constante de mola de 400   N / m está presa na parte de baixo de uma inclinação sem atrito de 30 ° . Um bloco de 500   g é pressionado contra a mola comprimindo a mola em 10   c m e depois é liberado. Qual é a velocidade no qual o bloco é lançado na inclinação?

Fica bonitinho? Fica sim! Então bora pra próxima.

Passo 4

b )

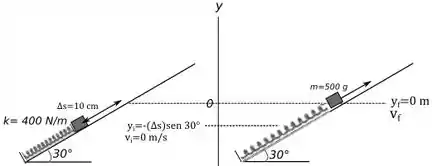
Passo 5

c ) Essa é bem simples pois é só resolver a equação do enunciado:

1 2 0,50   k g v f 2 =   ( 0,50   k g ) ( 9,80   m / s ² ) ( - 0,10   m s e n   30 ° ) + 1 2 ( 400   N / m ) ( - 0,10   m ) ²

Resolvendo:

1 2 0,50   k g v f 2 = - 0,245   k g   m 2 / s ² + 2   k g   m 2 / s ² → v f = 7,02   m 2 / s ² = 2,6   m / s

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma nuvem de cinzas vulcânicas está se movendo horizontalmente em solo plano quando encontra uma encosta com uma inclinação de 10 ° . A nuvem sobe 920m antes de parar. Suponha que os gases aprisionado
Uma lata de refrigerante de 2,50k g é lançada verticalmente para baixo de uma altura de 4,00m , com uma velocidade inicial de 3,00m / s . O arrasto do ar sobre a lata é desprezível. Qual é a energia c
Dois blocos, de massas M=2,0k g e 2 M , estão presos a uma mola de constante elástica k=200N / m que tem uma das extremidades fixa, como mostra a Fig. 8-67. A superfície horizontal e a polia não possu
Uma bola de 0,63k g , atirada verticalmente para cima com uma velocidade inicial de 14m / s , atinge uma altura máxima de 8,1m . Qual é a variação da energia mecânica do sistema bola Terra durante a s
Em 1981, Daniel Goodwin escalou 443m pela fachada do Edifício Sears, em Chicago, com o auxílio de ventosas e grampos de metal. (a) Estime a massa do alpinista e calcule a energia biomecânica (interna)