Para investigar as propriedades de um grande solenoide industrial, você conecta o solenoide e um resistor em série com uma bateria. As chaves permitem que a bateria seja substituída por um curto-circuito do solenoide e do resistor. Portanto, a Figura pode ser usada, com , em que é a resistência do solenoide e é a resistência do resistor em série. Com a chave aberta, você fecha e a mantém fechada até que a corrente no solenoide seja constante (Figura ). Depois, simultaneamente, é fechada e é aberta, usando um mecanismo de comutação com resposta rápida. Com um aparelho eletrônico de alta velocidade, você mede o tempo necessário para que a corrente diminua até metade de seu valor inicial. Essa medição é repetida para diversos valores de e obtêm-se estes resultados:

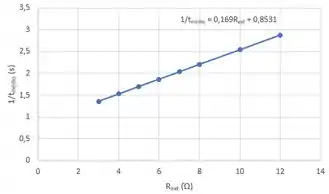
Desenhe um gráfico de seus dados na forma de em função de . Explique por que os pontos de dados desenhados dessa forma ficam próximos de uma linha reta. Use seu gráfico do item para calcular a resistência e a indutância do solenoide. Se a corrente no solenoide for , quanta energia está armazenada lá? A que taxa a energia elétrica está sendo dissipada na resistência do solenoide?
Passo 1
Vamos juntos detonar com essa questão!
A primeira coisa que o enunciado quer é o gráfico desse dados, até aí tudo bem, os pontos de vão ser os pontos do eixo e os pontos de são os pontos do eixo .
Em um circuito a corrente é dada pela seguinte expressão:
Os dados que o enunciado nos deu são para os instante onde temos a corrente igual a metade da que tínhamos inicialmente, assim:
Usando também que , a função da corrente fica da seguinte forma:
Agora podemos isolar e encontrar uma função referente ao gráfico que vamos fazer.
Então vamos poder comparar essa função com a função fornecida pelos parâmetros do gráfico e achar o valor de e .
Para encontrar a energia armazenada no solenoide pedida em podemos usar a seguinte equação:
Onde vamos usar o valor de que encontraremos em .
Esse item também quer saber a taxa de energia dissipada na resistência do solenoide. Taxa de energia é a mesma coisa que potência e a potência dissipada é dada por:
Onde no nosso caso vai .
Mãos à obra então!
Passo 2
Começando com o item . O nosso gráfico fica da seguinte forma:
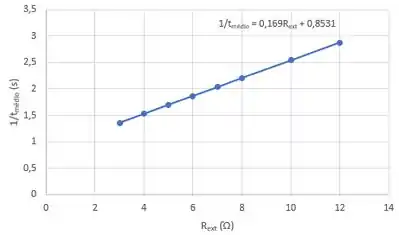
No passo chegamos em uma expressão que representava bem esses pontos, dada por:
Como tem uma dependência linear com o gráfico tende a ter esse comportamento de reta.
Passo 3
Agora vamos para o item .
Os pontos do gráfico nos fornecem a seguinte equação:
Comparando com a expressão que chegamos, temos que:
Da segunda equação podemos encontrar e conhecendo o valor dele podemos encontrar com a primeira equação. Vamos fazer essas contas!
Agora podemos encontrar .
Passo 4
E agora o item .
A energia armazenada no solenoide é dada por:
Substituindo os valores que conhecemos, temos:
Agora a potência dissipada é dada por:
Então:
Com isso finalizamos nossa questão com sucesso!
Resposta