Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 69

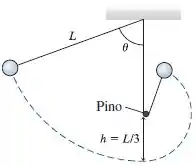
69. Um pêndulo é constituído por uma pequena esfera de massa m presa a um barbante de comprimento L . Como mostra a FIGURA PD10.69, a uma altura h = L / 3 em relação ao ponto mais baixo da trajetória normal do pêndulo, há um pino fixo. Qual é o mínimo valor do ângulo θ , a partir do qual o pêndulo é solto, para o qual a esfera conseguirá completar um círculo em torno do pino com o barbante esticado?

Passo 1

Então galera para encontrar o ângulo que o enunciado quer temos que achar a distância que a bolinha foi solta da plataforma onde ela está presa.

Para achar essa distância vamos considerar que o pino é nossa altura 0 , então temos que descobrir a que distancia do pino a bola é solta pois assim podemos subtrair essa distância de 2 L / 3 e encontramos a distância que ela foi solta da plataforma.

Com isso podemos formar um triangulo retângulo e teremos que:

cos ⁡ θ = y L

Para achar a distância da bola inicialmente do pino vamos usar a conservação de energia, mas para isso temos que saber a velocidade que abola deve ter no ponto mais alto da sua trajetória para que ela complete o círculo.

Para descobrir essa velocidade vamos usar a segunda lei de Newton, da seguinte forma:

F G + T = m v 2 r

Onde m v 2 / r é a força centrípeta que faz com que a bola faça o círculo. A força de tração T vai ser zero para que a corda se mantenha esticada e tenhamos a menor velocidade possível para que a bola complete o círculo. Assim:

F G = m v 2 r

Passo 2

Vamos então encontrar a velocidade que a bola deve ter para completar o círculo, temos:

F G = m v 2 r

⇒ m g = m v 2 r

⇒ g = v 2 r

Onde temos que o raio da trajetória é r = L / 3 , assim temos:

v 2 = g L 3

⇒ v = g L 3

Passo 3

Agora vamos fazer a conservação de energia onde a situação inicial é quando a bola ainda está em repouso e a situação final é o ponto mais alto da trajetória da bola, assim:

1 2 m v i 2 + m g y i = 1 2 m v f 2 + m g y f

Temos que a velocidade inicial é zero já que a bola parte do repouso. E a velocidade final é a velocidade que encontramos no passo anterior, assim:

m g y i = 1 2 m g L 3 + m g y f

⇒ y i = L 6 + L 3

⇒ y i = L 2

Passo 4

A distancia que encontramos no passo anterior é a distância da bola ao pino, então a distância da bola até o ponto que ela está presa, assim:

y = 2 L 3 - L 2 = L 6

Agora que temos essa distância podemos encontrar θ , temos:

cos ⁡ θ = y L

⇒ cos ⁡ θ = L / 6 L

⇒ cos ⁡ θ = 1 6

Então temos que:

θ = 80,4 °

Resposta

θ = 80,4 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mola ideal de massa desprezível tem 12,0 cm de comprimento quando nada está preso a ela. Ao pendurarmos um peso de 3,15 kg nessa mola, seu comprimento passa a ser 13,40 cm.Para que armazene 10,0 J
Uma mola armazena energia potencial U 0 quando está comprimida em uma distância x 0 em relação ao seu comprimento sem deformação. (a) Em termos de U 0 , quanta energia ela rmazena quando está comprimi
Considere o cavaleiro do Exemplo 7.7 (Seção 7.2) e a Figura 7.16. Como no exemplo, o cavaleiro é libertado a partir do repouso quando a mola está esticada 0,100 m. Qual é o deslocamento x do cavaleiro
Um queijo de 1,20k g é colocado sobre uma mola de massa desprezível e constante k = 1800N / m que está comprimida 15,0c m . Até que altura acima da posição inicial o queijo se eleva, quando a mola é l
a) Para o elevador do Exemplo 7.9 (Seção 7.2), qual era a velocidade do elevador quando ele desceu 1,0 m a partir do ponto 1 da Figura 7.17? b) Quando o elevador desceu 1,0 m a partir do ponto 1 da Fi