Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Problemas - Ex. 70
70. Depois que a corrente na Figura atinge seu valor estacionário final com a chave fechada e a chave aberta, a chave é fechada, colocando o indutor em curto-circuito. (A chave permanece fechada. Veja o Problema para os valores numéricos dos elementos do circuito.) Logo depois de a chave ser fechada, quais são os valores de e e quais são as correntes que passam em e ? Depois que a chave é fechada durante um tempo muito longo, quais são os valores de e e quais são as correntes que passam em e ? Determine as expressões para as correntes que passam em e em função do tempo desde o momento em que a chave é fechada. Seu resultado deve concordar com a resposta do item quando e com a resposta do item quando . Faça um gráfico dessas três correntes em função do tempo.
Passo 1
Bem, a parti do momento em que fechamos a chave podemos usar a lei de Ohm em e desconsiderar e o indutor já que estão em curto, mesmo que ainda haja uma corrente residual nessa parte, assim:
A corrente em ne instante vai ser dada pela diferença de pela corrente residual que passa por , já que é corrente total do circuito, assim:
A diferença de potencial em pode ser encontrada através da lei de Ohm também, tendo o valor da corrente .
A diferença de potencial é zero já que a parti do momento que foi fechada, a resistência e o indutor foram excluídos do circuito.
A corrente residual que mencionei acima presente entre e é igual como foi visto no exercício .
Depois de passado muito tempo da chave fechada a corrente continua com o mesmo valor já que não tem por que ela mudar de valor, logo a corrente em aumenta para o mesmo valor de e a diferença de potencial também.
A diferença de potencial continua com o mesmo valor de antes que é igual a zero, já que não tem por que ela mudar e a corrente que passa por agora vale zero já que essa pare pode ser considerada com excluída do circuito devido o fechamento de .
Passo 2
Primeiro vamos encontrar o que é pedido no item .
Vamos então encontrar , temos:
Substituindo os valores que conhecemos temos:
Tendo isso a corrente em é dada por:
O valor de é dada por:
E o valor de como foi dito no passo é zero.
Passo 3
Agora vamos o que é pedido no item .
Temos que a corrente se matem a mesma coisa, a corrente em sobe para o mesmo valor de e a corrente em vai a zero.
A diferença de potencial continua a mesma e a diferença de potencial continua zero.
Passo 4
Agora vamos encontrar funções para e .
Primeiro para temos que ela se manteve constante a todo momento, então ela não depende .
Para vemos que ela é uma corrente em decaimento em uma parte do circuito que podemos considerar um circuito , assim ela apresenta o seguinte comportamento segundo a equação .
Onde é a soma das resistências do circuito, assim:
E do exercício temos que , assim nossa equação fica:
Agora para achar uma função para , vamos usar uma relação que usamos antes, dada por:
Substituindo com o que sabemos, temos:
Passo 5
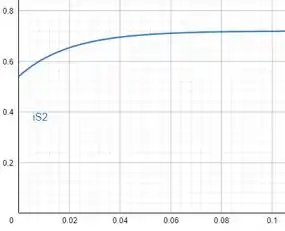
Os gráficos das funções de , e , estão mostrados abaixo.
Para temos:
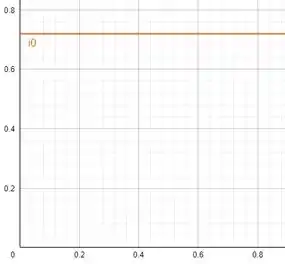
Para , temos:
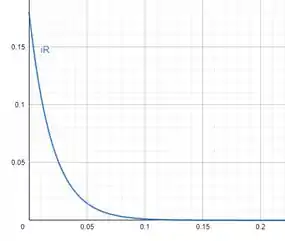
Para , temos:
